중학생이 풀어보는 수능 수학 - 2025학년도 대학수학능력시험 수학영역 3번, 등비수열의 정의와 특징을 활용하여 풀어보자.

728x90

2025학년도 대학수학능력시험 수학영역 3번 (2025. 11. 14.)

이전 포스팅에서 이어지는 내용입니다

https://wkqtkdtlr.tistory.com/414

중학생이 풀어보는 수능 수학 - 2025학년도 대학수학능력시험 수학영역 3번, 수열이란? 등비수열

---

정의를 활용하여 문제를 풀어보자

지난 포스팅에서 첫째항을 a, 공비를 r로 가지는 등비수열의 n번째 항은 다음과 같이 표현할 수 있음을 알아보았다

$$ a_n = ar^{n-1} $$

이를 이용하여 문제를 풀어보도록 하자. 문제를 보면 첫째항과 공비가 모두 양수 k인 등비수열 {$a_n$}이라고 하니, 이를 위의 식과 같이 바꾸면

$$ \begin{align} a_n & = k \cdot k^{n-1} \\ \\ & = k^{1+n-1} \\ \\ & = k^n \end{align} $$

(지수법칙과 관련해서는 해당 포스팅을 참고)

 

따라서 문제에 나온 식은 다음과 같이 바꿔서 표현할 수 있다.

$$ \begin{align} \frac{a_4}{a_2} + \frac{a_2}{a_1} & = \frac{k^4}{k^2} + \frac{k^2}{k^1} \\ \\ & = k^{4-2} + k^{2-1} \\ \\ & = k^2 + k = 30 \end{align} $$

무언가를 나눌 때는 반드시 "정말 나누어도 되는가?"를 항상 의심해야 한다. 즉, 0으로 나눈 것은 아닐까? 라는 의심을 항상 하는 것이 수학이라는 논리학을 공부하는 데 있어서 당연한 수순이다. 왜냐하면 분수라는 것은 분모가 0이 아닐 때 정의하는 것을 기본으로 하기 때문

 

그렇기 때문에, 문제에서는 첫째항과 공비로 쓰인 k가 양수, 즉, $ k > 0 \Rightarrow k \neq 0 $임을 조건으로 제시하는 것이다. k가 0이 아니기 때문에 $k^n$은 항상 0이 아니므로, 위의 식대로 문제를 풀어도 이상이 없다. 너무나도 당연한 이야기인 듯하지만, 이를 한번 짚을 줄 아는 것과 모르는 것은 수학의 기초를 다지는데 엄청난 차이를 가져온다.

 

결국 문제에서 주어진 식은 $ k^2 + k = 30 $이라는 부등식의 해를 구하라는 것과 같다. 이차방정식을 풀어보면

$$ \begin{align} & k^2 +  k = 30 \\ \\ \Rightarrow \; & k^2 + k - 30 = 0 \\ \\ \Rightarrow \; & (k+6)(k-5) = 0 \\ \\ \Rightarrow \; & k = 5, \; k = -6 \end{align} $$

하지만 문제에서 $k>0$이라고 하였으므로 $k=5$, 답은 ⑤이다. 

 

등비수열의 성질을 이용하여 문제를 풀어보자

물론 등비수열의 정의를 이용한 위의 풀이가 가장 원칙적인 방법일 수도 있겠지만, 사실 등비수열이 어떻게 만들어지는지에 대한 생각을 조금만 해본다면, 더 쉽게 문제를 풀 수 있다. 

 

이전 포스팅에서도 이야기했지만, 등비수열이라는 것은 결국 같은 비율(공비)로 계속 변화하는 수열이다. 문제에서 공비는 k라고 하였으므로 아래와 같이 표현이 가능하다. 

여기에서 분수의 의미를 한번 되새겨보자. 분수라는 것은 $ \dfrac{a}{b} $형태의 수를 말한다는 것은 누구나 아는 이야기이지만, 이것은 실제로 무엇을 의미하는 것일까? 

 

$$ \frac{a}{b} = m \; \Leftrightarrow \; a = mb \;\; (b \neq 0) $$

 

$ \dfrac{a}{b} = m $이라는 것은, $b$가 $a$로 되기 위해서는 $m$배가 필요하다는 것을 의미한다$(\Rightarrow a = mb)$. 그렇다면 문제에서 제시한 분수인 $\dfrac{a_2}{a_1}$을 같은 방식으로 표현하면

 

"$\dfrac{a_2}{a_1} = p \; \Rightarrow $ $a_1$이 $a_2$로 되기 위해서는 $p$배가 필요하다."

 

같은 방식으로 $\dfrac{a_4}{a_2}$도 표현하면,

 

"$\dfrac{a_4}{a_2} = q \; \Rightarrow $ $a_2$가 $a_4$로 되기 위해서는 $q$배가 필요하다."

 

그렇다면 위의 문제는 이제 "$p$와 $q$가 무엇이냐?"로 바뀌게 된다. 다만 이는 위에서 언급한 등비수열의 특징을 통해 직관적으로 알 수 있다. 

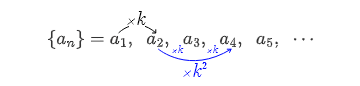
즉, $a_1$이 $a_2$가 되기 위해서는 k배 하여야 하고, $a_2$가 $a_4$로 되기 위해서는 $k^2$배가 필요하다. 즉 $p = k, \; q = k^2 $ 이므로 

$$ \begin{align} \frac{a_4}{a_2} + \frac{a_2}{a_1} & = p + q \\ \\ & = k^2 + k \\ \\ & = 30 \end{align} $$

으로 바로 직관적으로 유추할 수 있다. p와 q는 설명을 위해서 추가했을 뿐이지, 실제로 생각하고 문제를 풀어나갈때는 바로 유추가 가능하다.

 

이후 2차방정식 풀이과정은 위와 동일하므로 생략