2025학년도 대학수학능력시험 수학영역 2번 (2025. 11. 14.)

이전 포스팅에서 이어지는 내용입니다.
https://wkqtkdtlr.tistory.com/382
중학생이 풀어보는 수능 수학 - 2025학년도 대학수학능력시험 수학영역 2번, 수열의 극한이란? 그
2025학년도 대학수학능력시험 수학영역 2번 (2025. 11. 14.)이전 포스팅에서 이어지는 내용입니다.https://wkqtkdtlr.tistory.com/381 중학생이 풀어보는 수능 수학 - 2025학년도 대학수학능력시험 수학영역 2
wkqtkdtlr.tistory.com
┃함수안에서 수열을 만들어보자
이전 포스팅에서 정의했던 함수의 극한을 다시 한번 살펴보자.
$$ x가 한없이 a에 가까워질 때, f(x)가 한없이 L에 가까워지면,\; \lim_{x \to a}f(x) = L $$
지난 포스팅을 통해 "x가 a에 한없이 가까워진다."라는 개념이 어떤 것인지 대략적으로 이해는 했을 것이다. 어떤 수열 a(n)이 n이 무한히 커짐에 따라 L로 수렴한다고 하면, n이 커질수록 a(n)과 L과의 거리가 점점 가까워져서 거의 같게 되는데, 이를 lim라는 기호를 통해 이를 같은 것으로 정의하겠다고 했다.
그럼 이를 자연수 n이 아닌 실수 x, 그리고 이 x는 f(x)라는 관계를 갖는 함수라고 가정해보자.
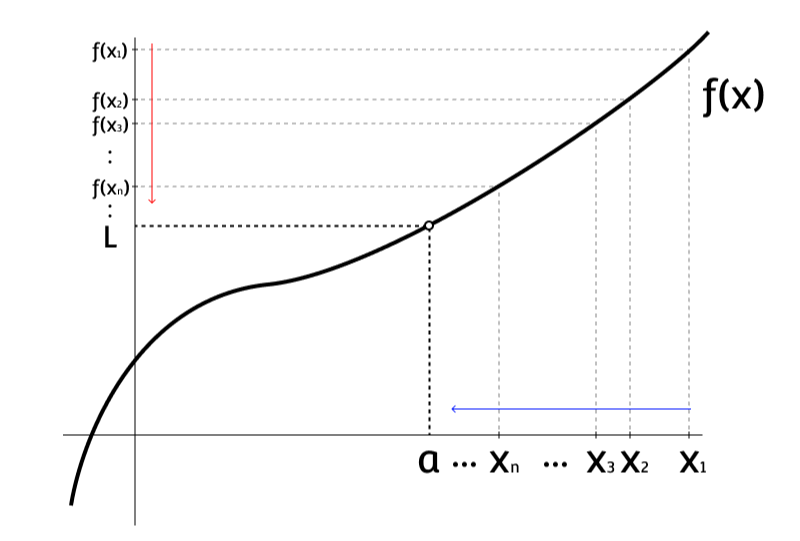
선행학습을 했다면 어디에서 많이 봤을 법한 그림일 것이다. 여기에서 우리는 X(n)이라는 수열을 다음과 같이 정의하고자 한다.
$$ X_n = \{x_n \, | \, x_n은 \, a와 \,x_{n-1} 사이의 \, 임의의 \, 실수, \; x_1 > a, \; n \in \mathbb{N} \} $$
먼저, a보다 큰 어떤 임의의 실수 x(1)을 정한다. 그리고 나서 a와 x(1) 사이의 실수 중 내맘대로 실수를 골라 이를 x(2)라고 하면,
$$ a < x_2 < x_1 $$
x(2)의 크기는 위와 같이 정의할 수 있다. x(3) 역시 이렇게 결정한 x(2)와 a 사이의 실수 중 내맘대로 실수를 골라 이를 x(3)라고 하고
$$ a < x_3 < x_2 < x_1 $$
을 만족하게 된다. 이를 계속 반복하게 되면,
$$ a < \cdots < x_n < \cdots < x_2 < x_1 \quad \cdots (1) $$
이 되므로, 모든 항에 a를 빼더라도 그 크기의 관계는 변하지 않으므로
$$ a - a = 0 < \cdots < x_n - a < \cdots < x_2 - a < x_1 - a $$
모든 값이 0보다 크기 때문에 그 절댓값을 취해도 크기의 관계는 똑같이 변하지 않으므로,
$$ 0 < \cdots < |x_n - a| < \cdots <|x_2 - a| < |x_1 - a| $$
즉, n이 커지면 커질수록 a와 한없이 가까워지는 모양을 하게 된다. X(n)이라는 수열은 결국 n이 무한히 커질 수록 a에 한없이 가까워진다. 이를 지난 포스팅에서 우리는 다음과 같이 표현하기로 했었다.
$$ \lim_{n \to \infty} X_n = a $$
수열이라는 것은 반드시 무슨 수식으로 나타낼 수 있는 정형화된 관계를 가져야 할 필요는 없다. 위와 같이 수열을 정의해도 전혀 이상할 것이 없고, 또한 이렇게 정의할 경우 X(n)이라는 수열이 a에 한없이 가까워진다는 사실 역시 지난 포스팅을 통해 lim로 정의할 수 있음도 알게 되었다. (엄밀히 말하자면 우극한이지만...)
여기에서 우리가 정한 X(n)의 구성원들은 이와 관련된 함수 f(x)를 만족하기도 하다. 따라서 각각의 x(n)들은 그에 대응하는 f(x(n))이 존재한다(함수와 관련된 내용은 해당 포스팅을 참고)
$$ x_1 \to f(x_1) ,\; x_2 \to f(x_2) ,\; \cdots , \; x_n \to f(x_n), \cdots $$
┃우리가 알고 싶은 것은 결국 f(x)→L이다.
하지만 우리가 알고 싶은 것은 x(n)의 수렴이 아니라 f(x)의 수렴,
$$ \lim_{x \to a} f(x) = L $$
결국 f(x)가 L에 한없이 가까워지는지가 궁금하다는 것이 포인트. 우리는 이전 수열의 극한과 관련된 포스팅에서 한없이 가까워진다는 것은 그 거리가 가까워진다는 것, 그리고 수학에서의 거리는 절댓값임을 강조했었다. 그럼 이와 관련하여 다음의 그림을 살펴보자.

위의 f(x)라는 함수의 그래프를 잘 살펴보면, a보다 큰 구간에서는 함수가 계속 감소하고 있기 때문에, f(x(n))은 n이 커지면 커질수록 L이 있는 방향으로 지속적으로 감소하게 된다.
$$ f(x_1) > f(x_2) > \cdots > f(x_n) > \cdots > L $$
그리고 위에서 (1)식을 다시 살펴보면
$$ x_1 > x_2 >\cdots > x_n > \cdots > a $$
그렇다면, 아주아주 큰 자연수 임의의 N에 대해서 이보다 큰 자연수 m이 존재한다면,
$$ x_N > x_m > a \quad \Rightarrow \quad |x_N - a| > |x_m - a| \cdots (2) $$
을 만족하므로, 이에 대응되는 f(x(N))과 f(x(m)) 역시
$$ f(x_N) > f(x_m) > L \quad \Rightarrow \quad |f(x_N) -L| > |f(x_m) -L| \cdots (3) $$
를 만족한다.
수열의 극한에서 살펴봤을 때와 마찬가지로 N은 내마음대로 정한 아주아주 큰 자연수이고 그것보다 큰 자연수 m에 대해서 위의 (2), (3)을 만족하기 때문에, m을 다시 N으로 놓고 그것보다 더 큰 자연수 m을 정하더라도 (2), (3)을 또 만족하게 된다. 즉, 이를 무한히 반복하게 되면 위 절댓값들은 한없이 작아지게 된다.
$$ |x_N - a| \to 0 \quad \Rightarrow \quad |f(x_N) - L| \to 0 $$
이건 함수가 계속 감소하고 있기 때문에 나타나는 성질이 아닌가? 라고 할 수 있겠지만, 함수가 계속 증가하고 있는 경우에도 똑같은 방법으로 증명할 수 있다. 따라서, 함수가 계속 감소하거나, 계속 증가하는 경우에는 모두 위와 같이 절댓값에 따라 한없이 가까워진다고 정의할 수 있게 된다.
하지만 함수가 지속적으로 증가하거나 감소하는 경우가 오히려 특이한 경우이지, 함수의 대부분은 증감이 계속적으로 변하기 마련인데, 왜 그런 특이한 경우만을 놓고 이야기를 하고 있는 것일까?

우리는 어차피 a에 한없이 가까워질때의 f(x)의 모습이 궁금한 것이므로, a와 멀리 떨어진 곳들은 사실 고민할 이유가 없다. 그렇다면 a의 주변은 아주 짧을지라도 반드시 계속 증가하거나, 계속 감소하는 구간이 존재하게 된다. 위의 그림을 보면 f(x)는 아주 촘촘히 진동하고 있음에도 결국 확대해보면 a주변의 아주아주 짧은 범위 안에서 계속 감소하거나 계속 증가하는 구간만을 따로 뽑아낼 수 있다.
x가 a로 한없이 가까워진다는 것은 이 구간보다도 아주아주 짧은 거리로 가까워지는 상태를 이야기하는 것이므로, 해당 구간만을 놓고 생각하더라도 극한의 입장에서는 전혀 문제될 것이 없다. 결국 항상 감소하거나 항상 증가하는 함수에 관해서만 생각하더라도 모든 함수에 대한 극한을 생각하는 것과 다름이 없다는 것이다.
결국, x가 a에 계속 가까워지는 X(n) 수열을 만들어 그에 대응하는 f(X(n)) 수열을 만들었더니, f(X(n))이 L에 한없이 가까워지게 되었다. 하지만 x는 a가 아니므로 그에 대응하는 f(x)도 L이 아닌 것처럼 보인다. 따라서 수열의 극한 때와 같이, 이를 lim라는 기호를 통해 같다고 표현하기로 하자
"x가 a에 한없이 가까워질 때, f(x)가 L에 한없이 가까워지면"
$$ \lim_{x \to a} f(x) = L $$
라고 정의하게 된다.
┃함수에서 극한이 존재한다는 것은?
x가 a에 한없이 가까워진다는 의미를 다시 한번 살펴보자.

애초에 수열 a(n)의 경우에는 그 구성원이 모두 양수였기 때문에 당연히 양수쪽에서 다가오는 것만 생각하면 됐지만, 함수에서는 그렇지 않다. 특별한 경우가 아니라면 대부분의 함수는 정의역의 구간이 한쪽 방향이기보다는 양방향에서 정의가 된다. 지금까지 위에서 우리가 살펴본 것은 x > a일 경우로 이를 "우(右)극한"이라고 한다. 똑같은 방식으로 왼쪽에서 a로 한없이 가까워지는 경우 역시 정의할 수 있으므로, 이를 따로 설명하지는 않고 이를 "좌(左)극한"이라고 한다는 사실만 짚고 넘어가도록 한다.
그렇다면, 함수 f(x)는 x가 a에 한없이 가까워질 때, f(x)도 어떤 값으로 가까워지기만 하면 함수값을 가질까?

첫번째 함수의 경우 x가 a의 왼쪽에서 다가올 때는 L₁으로 가까워지고 있지만, a의 오른쪽에서 다가올 때는 L₂로 가까워지고 있다. 둘 다 정의에 의하면, 다음과 같이 표현할 수 있다. a보다 작은 쪽에서 접근하는 것은 a-, 큰 쪽에서 접근하는 것은 a+ 라고 표현하면 아래와 같다.
$$ \lim_{x \to a-} f(x) = L_2 , \quad \lim_{x \to a+} f(x) = L_1 $$
하지만 실제로 L₁과 L₂는 서로 다른 값이므로, 접근하는 방향에 따라 L₂를 좌극한 L₁을 우극한이라고 다르게 표현하기로 약속한다. 이 때 첫번째 함수의 경우에는 x가 a에 한없이 가까워질 때, 좌극한과 우극한이 서로 다르다.
하지만, 첫번째 함수와는 달리 두번째 함수는 첫번째와 달리 좌극한과 우극한이 모두 같다.
$$ \lim_{x \to a-} f(x) = \lim_{x \to a+} f(x) = L $$
즉, x가 a로 어떤 방향에서 접근하더라도 f(x)는 항상 같은 값으로 수렴함을 의미한다. 우리는 이럴 때(좌극한과 우극한이 서로 같을 때) 극한이 존재한다고 표현한다.
$$ \lim_{x \to a} f(x) = L \quad \Leftrightarrow \quad \lim_{x \to a-} f(x) = \lim_{x \to a+} f(x) = L $$
┃함수의 극한값이 존재한다면, 그 값은 함수값과 일치하는가?
다시 맨 위의 <그림 1>을 한번 살펴보자. 지겹도록 "x가 a에 한없이 가까워질 때, f(x)가 L에 한없이 가까워진다"고 표현했지만, 아무리 눈씻고 다시 봐도 결국 L은 결국 x가 a일 때의 함숫값, 즉, f(a)로 보이지 않는가? 그러면 그냥 f(a)라고 표현하면 되지 왜 지금까지는 쭉 L이라는 임의의 실수를 두고 이 L에 가까워진다고 가정해왔을까?
아래와 같은 함수를 예로 들어보자.
$$ f(x) = \frac{x^2-1}{x-1} $$
이 함수는 사실 x+1과 같은 함수처럼 보인다.
$$ \begin{align} f(x) & = \frac{x^2 - 1}{x-1} \\ \\ & = \frac {(x+1)(x-1)}{x-1} \\ \\ & = x+1 \end{align} $$
하지만 x+1과 가장 큰 차이점이 있는데 바로 x가 1에서 정의되지 않는다는 것이다. 왜냐하면, 분모에 x-1이 있기 때문에 x가 1이 되면, 0으로 나누게 되는 오류가 생기기 때문이다. 따라서 위의 f(x)는 사실 다음과 같은 조건이 숨겨져 있는 것과 다름이 없다.
$$ f(x) = \frac{x^2-1}{x-1}, \quad (x \ne 1, \, x \in \mathbb{R}) $$
따라서 이를 그래프로 그려보아도 다음과 같이

x가 1에서 정의되지 않기 때문에 x = 1에서 구멍이 뚫려있게 된다. 그럼 이 f(x)에 대해서 x가 1에 한없이 가까워질 때, f(x)는 어떤 값으로 가까워지는가?
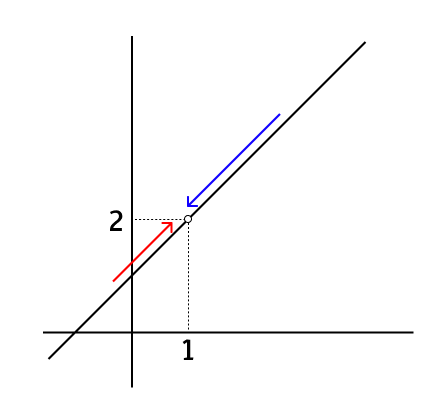
그냥 직관적으로 살펴보아도, x가 1에 한없이 가까워지면 그 f(x)값은 2에 가까워짐을 알 수가 있다. 그래프가 아니라면 다음과 같이 직접 계산해보도록 하자
| x | 1.01 | 1.001 | 1.0001 | … | 1.000000000001 |
| f(x) | 2.01 | 2.001 | 2.0001 | … | 2.000000000001 |
x가 1에 가까워질수록 그 f(x) 역시 2에 가까워짐을 알 수 있다.
좌극한의 경우도 마찬가지로 직관적으로 확인할 수 있으므로 우리는 다음과 같이 정의할 수 있다.
$$ \lim_{x \to 1-}f(x) = \lim_{x \to 1+} f(x) = 2 $$
하지만 f(1)은 정의되지 않기 때문에
$$ f(1) \ne 2 $$
이므로, x가 1에 가까워진다고 하여 그 함숫값이 f(1)로 항상 수렴하는 것은 아니다.
위 함수의 특징은 x=1에서 정의되지 않는다는 것으로 그래프에서도 알 수 있듯이 함수가 x=1에서 쭉 이어지지 않고 끊어지게 된다는 특징이 있다. <그림 2>에서 왼쪽 함수를 살펴보아도 좌극한과 우극한이 달라 극한이 존재하지 않았던 경우 역시 그래프가 쭉 이어지지 않고 끊어진다는 특징이 있다. 이렇게, 그래프를 한붓그리기마냥 한번에 쭉 이어지는 것이 아니라 어떤 지점에서 툭 끊어지게 된다면, 그런 그래프들은 극한값이 존재하지 않거나, 존재하더라도 함숫값과 일치하지 않는다는 특징을 가지게 된다.
그럼 반대로 그래프들이 끊어지는 지점이 없다면? 위의 f(x)가 x=1에서도 정의가 되는
$$ f(x) = x+1, \, (x \in \mathbb{R}) $$
이라면 어떨까?

이번에는 반대로 x=1에서 f(x)가 정의되기 때문에 다음과 같이 표현할 수 있다.
$$ \lim_{x \to 1-}f(x) = \lim_{x \to 1+}f(x) = 2 = f(1) $$
좌극한과 우극한이 모두 f(1)로 수렴하므로
$$ \lim_{x \to 1}f(x) = f(1) $$
이라고 할 수 있다. 위에서는 x=1일때 함수가 정의되지 않기 때문에 x=1의 경우만 살펴보았지만, 지금의 f(x)는 하나의 직선으로 쭉 이어져 있기 때문에, x는 임의의 구간 모두에서 다음과 같이 정의할 수 있다.
$$ \lim_{x \to a} f(x) = f(a), \, (a \in \mathbb{R}) $$
우리는 이렇게 함수의 정의역 구간 전체에서 그 극한값이 함숫값과 일치한다면, 위에서 살펴본 바와 같이 끊어진 구간이 없으므로, 이를 "연속한다."라고 표현한다.
$$ f(x)는 \, a에서 \, 연속이다. \, \Leftrightarrow \, \lim_{x \to a} f(x) = f(a) $$
지금까지 살펴본 내용들은 엄밀한 수학적인 정의는 아니다. 본래 극한의 정의는 "엡실론-델타 논법"을 통해 증명한다. 하지만 이는 고교과정을 아득히 뛰어넘는 개념이므로, 고교과정 내에서는 다음과 같이 정의하도록 하자.
"f(x)가 연속이다 ⇔ 모든 x에 대해서 좌극한, 우극한, 함숫값이 모두 일치한다."
즉, f(x)가 x는 a에서 연속이라면, a에서의 f(x)의 극한값은 f(a)로 쉽게 구할 수 있다. 이를 이용하여 2번 문제를 이제 풀어보도록 하자.
다음 글
https://wkqtkdtlr.tistory.com/408
중학생이 풀어보는 수능 수학 - 2025학년도 대학수학능력시험 수학영역 2번, 함수의 극한의 성질
2025학년도 대학수학능력시험 수학영역 2번 (2025. 11. 14.) 이전 포스팅에서 이어지는 내용입니다.https://wkqtkdtlr.tistory.com/385 중학생이 풀어보는 수능 수학 - 2025학년도 대학수학능력시험 수학영역 2
wkqtkdtlr.tistory.com
'수학 이야기' 카테고리의 다른 글
| 중학생이 풀어보는 수능 수학 - 2025학년도 대학수학능력시험 수학영역 3번, 수열이란? 등비수열과 공비란 무엇인가? (0) | 2025.01.05 |
|---|---|
| 중학생이 풀어보는 수능 수학 - 2025학년도 대학수학능력시험 수학영역 2번, 함수의 극한의 성질과 연속함수의 성질, 문제 풀이 (1) | 2024.12.31 |
| 중학생이 풀어보는 수능 수학 - 2025학년도 대학수학능력시험 수학영역 2번, 수열의 극한이란? 그리고 극한의 의미는? (2) | 2024.11.17 |
| 중학생이 풀어보는 수능 수학 - 2025학년도 대학수학능력시험 수학영역 2번, 함수와 수열이란? (1) | 2024.11.17 |
| 중학생이 풀어보는 수능 수학 - 2025학년도 대학수학능력시험 수학영역 1번 문제 풀이 (2) | 2024.11.15 |

