2025학년도 대학수학능력시험 수학영역 2번 (2025. 11. 14.)

이전 포스팅에서 이어지는 내용입니다.
https://wkqtkdtlr.tistory.com/381
중학생이 풀어보는 수능 수학 - 2025학년도 대학수학능력시험 수학영역 2번, 함수와 수열이란?
2025학년도 대학수학능력시험 수학영역 2번 (2025. 11. 14.)우리가 지수의 개념을 자연수 → 유리수로 확장 을 한 것처럼, 함수도 지수의 개념과 같이 자연수 → 실수로 확장(엄밀한 개념으로는 정의
wkqtkdtlr.tistory.com
┃수열의 극한이란?
우선 극한을 설명하면서 다루는 내용은 교육과정 외의 내용이므로, 이것이 이해되지 않는다고 하더라도 가볍게 읽을 수 있을 만큼만 소개하고자 한다. 먼저 교육과정 수학Ⅱ에서 극한을 어떻게 정의하는지 살펴보자
$$ x가 한없이 a에 가까워질 때, f(x)가 한없이 L에 가까워지면,\; \lim_{x \to a}f(x) = L $$
이 정의에서 "한없이 ○에 가까워진다."라는 말이 너무나도 애매모호한 표현이기에, 단순히 감으로만 정의하던 것을 교육과정 외의 내용을 소개함으로써 정의해보고자 한다.
이전 포스팅에서 수열의 극한이 선행되어야 한다고 했으므로 우선 모든 설명은 수열의 극한에서부터 시작.
우리가 참고할 수열은 바로
$$ a_n = \frac{1}{n}, \; (n \in \mathbb{N}) $$
이 수열은 1부터 시작해서 1/2, 1/3, … 로 무한히 이어지는 수열이다. 우선 직관적으로 살펴보기 위해 수직선 위에서 이를 놓고 비교해보자.
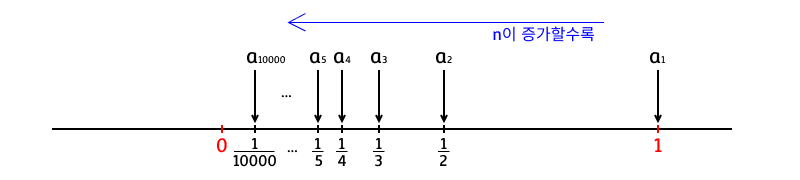
잘 보면, 이 수열은 1에서부터 시작해서 n이 증가함에 따라 점점 0에 가까워지는 모습을 보이고 있다. 우선 n은 자연수이므로
$$ n>0 \;\Rightarrow\; \frac{1}{n} > 0 $$
임은 당연하기에, 이 수열이 0보다 작아질 일은 없다. 그렇다면, 이 수열이 "한없이 0에 가까워진다."라는 것은 무엇을 의미하는 것일까? 아래 그림을 살펴보자.

아주아주 큰 임의의 자연수 N이 존재할 때 수열의 N번째 항목(이하 a(N) 형태로 표시한다.)은 다음과 같이 표현할 수 있다.
$$ a_N = \frac{1}{N} \quad (N은\,아주아주\,큰\,자연수)$$
자연수는 무한하기 때문에 아무리 아주아주 큰 자연수 N을 가정했다더라도, 그보다 큰 자연수 m은 항상 존재하게 된다.
$$ N<m \quad (N, m \in \mathbb{N}) $$
우리는 분수의 크기를 비교할 때, 분자가 서로 같다면 분모가 큰 쪽이 작은 수임을 알고 있다. 따라서 m이 N보다 큰 자연수라면, 분자가 1로 서로 같은 1/m과 1/N의 크기를 비교할 경우 1/m은 1/N보다 작은 수가 된다.
$$ \begin{align} N<m \; & \Rightarrow \; \frac{1}{N} > \frac{1}{m} \\ \\ & \Rightarrow \; a_N > a_m \end{align} $$
여기에서 "a(m)이 a(N)보다 작다."라는 것은 무엇을 의미하는지에 대해서 조금 심도있게 짚어 볼 필요가 있다.
┃"○에 한없이 가까워진다."라는 것은 ○과의 거리가 아주 가깝다는 것이다.
양수에서 어떤 수가 작다는 것은 여러분들에게는 어떤 의미인가? 2가 3보다 작다는 것은 단순히 그 크기가 작은 것일 수도 있고, 자연수 순서상 2가 3보다 먼저 나오니 2가 작다는 것일 수도 있으며, 2에서 3을 빼면 -1로 0보다 작은 수가 되니 2가 작다고 표현하는 사람도 있을 것이다. 아니면 너무나도 당연한 이야기인지라, 이에 대해서 생각조차 안해봤을 것이다.
하지만 극한으로의 접근을 위해 어떤 수가 작다는 것을 우리는 다음과 같이 따로 정의하고자 하는데,
"어떤 수가 작다라는 것은 수직선상에서 그 수가 0에 더 가까이 있다는 것이다."
위의 그림 1을 보면 알 수 있듯이, 1/m이 1/N보다 0에 더 가까운 것을 알 수 있다. 우리는 중등교육과정에서 어떤 수와의 거리를 표현할 때에 "절댓값"을 이용한다는 것을 이미 배웠으므로,
$$ |0 - \frac{1}{N}| > |0-\frac{1}{m}| \quad (N < m)$$
으로 표현할 수 있다.
즉, 임의의 아주아주 큰 자연수 N이 있더라도 그보다 큰 자연수 m은 항상 존재하므로, a(N)보다 0에 가까운 수열의 구성원 중 하나인 a(m)이 반드시 존재한다는 것을 의미한다. 이 때의 m도 아주아주 큰 자연수이니 N으로 다시 바꿔볼 수 있고, 그 N보다 큰 자연수 m은 또다시 존재하여 이 a(N)보다 0에 가까운 a(m) 역시 또다시 존재하게 된다. 이렇게 무한히 반복하게 되면, 결국 N이 무한히 커지면 커질수록 a(N) = 1/N은 점점 0에 가까워지는 수가 되고, 결국 1/N과 0의 거리는 아주아주아주 짧은 거리가 될 것이다.
$$ \begin{align} N \to \infty \; & \Rightarrow \; |0 - a_N| \to 0 \\ \\ & \Rightarrow \; a_N = \frac{1}{N} \approx 0 \end{align} $$
마지막 수식만을 다시 살펴보자.
$$ \frac{1}{N} \approx 0 $$
하지만 N은 아주아주 큰 수이긴해도, 어찌됐든 0은 아니므로, 1/N은 절대 0이 될 수 없다. 그런데 N이 한없이 커지면 커질 수록 1/N = a(N)과 0은 계속 가까워지게 된다.
수학자들은 "N이 커질수록 1/N은 0에 가까워진다."라는 애매모호한 표현보다는 "N이 무한이 커지면, 1/N은 0이다!"라고 명확히 표현하기를 바란다. 하지만 처음에 이야기했듯이 당연히 1/N은 0이 될 수 없다. 그래서 lim라는 기호를 통해 다음과 같이 표현하기로 한다.
"n이 무한히 커질 수록, a(n)은 계속 작아져서 0과의 거리가 좁아진다."
↓
"n이 무한이 커질수록, a(n)이 0에 한없이 가까워진다."
그리고 이것을 다음과 같이 표현하기로 한다.
$$ \lim_{n \to \infty} \frac{1}{n} = \lim_{n \to \infty} a_n = 0 $$
지금까지 살펴본 내용을 0은 L로 바꾸고, 수열 a(n)이 1/n이 아닌 임의의 어떤 수열이라고 바꿔보자. "a(n)이 L에 한없이 가까워진다, 수렴한다."는 의미는 결국 아래와 같다.
"n이 무한히 커질 수록, a(n)이 L에 한없이 가까워진다."
↓
$$ \lim_{n \to \infty} a_n = L $$
라고 표현할 수 있고, 이 속에 내재된 뜻은 n이 무한히 커질수록
$$ a_n \to L \; \Rightarrow \; |L - a_n| \approx 0 \quad (n \to \infty, n \in \mathbb{N}) $$
를 의미한다는 점을 반드시 기억하도록 하자.
사실 지금까지 다룬 내용은 교육과정 내의 이야기는 아니기 때문에, 완벽히 이해하기도 어려울 것이다. 다만, 극한에서 "한없이 가까워진다."라는 것이 단순한 단어의 의미 그대로의 가까움을 이야기하는 것이 아니라 수학적인 거리인 "절댓값"이 0에 가까워짐을 의미한다는 사실을 인지하고 있는 것만으로도 앞으로의 극한을 이해하는 데에는 아주 큰 도움이 될 것이다.
그와 동시에 아래 수열의 극한값은 위에서 계속 살펴보았으므로, 외워두고 가자.
$$ \lim_{n \to \infty} \frac{1}{n} = 0, \;(n \in \mathbb{N}) $$
다음 글
https://wkqtkdtlr.tistory.com/385
중학생이 풀어보는 수능 수학 - 2025학년도 대학수학능력시험 수학영역 2번, 함수의 극한이란? 좌
2025학년도 대학수학능력시험 수학영역 2번 (2025. 11. 14.)이전 포스팅에서 이어지는 내용입니다.https://wkqtkdtlr.tistory.com/382 중학생이 풀어보는 수능 수학 - 2025학년도 대학수학능력시험 수학영역 2
wkqtkdtlr.tistory.com
'수학 이야기' 카테고리의 다른 글
| 중학생이 풀어보는 수능 수학 - 2025학년도 대학수학능력시험 수학영역 2번, 함수의 극한의 성질과 연속함수의 성질, 문제 풀이 (1) | 2024.12.31 |
|---|---|
| 중학생이 풀어보는 수능 수학 - 2025학년도 대학수학능력시험 수학영역 2번, 함수의 극한이란? 좌극한, 우극한 그리고 연속함수가 갖는 의미 (0) | 2024.11.22 |
| 중학생이 풀어보는 수능 수학 - 2025학년도 대학수학능력시험 수학영역 2번, 함수와 수열이란? (1) | 2024.11.17 |
| 중학생이 풀어보는 수능 수학 - 2025학년도 대학수학능력시험 수학영역 1번 문제 풀이 (2) | 2024.11.15 |
| 중학생이 풀어보는 수능 수학 - 2025학년도 9월 모평 1번 문제 풀이와 답 (1) | 2024.11.11 |


