2025학년도 대학수학능력시험 9월 모의평가 (2024. 9.)

이전 포스팅에서 이어지는 내용이므로 이전 내용을 읽고 오는 것을 추천합니다.
https://wkqtkdtlr.tistory.com/376
중학생이 풀어보는 수능 수학 - 2025학년도 9월 모평 1번 문제, 제곱근의 개념과 지수의 확장(정수
2025학년도 대학수학능력시험 9월 모의평가 (2024. 9.) 지난 포스팅에 이어지는 내용입니다. 반드시 읽고 오시기 바랍니다. 중학생이 풀어보는 수능 수학 - 2025학년도 9월 모평 1번 문제, 거듭제곱
wkqtkdtlr.tistory.com
┃지금까지의 정의를 통해서 문제를 풀어보자
우리는 지금까지의 포스팅을 통해 p가 유리수 일 때, a의 p승과 루트에 대해서 정의할 수 있게 되었다. 이제 이 정의를 이용해서 2025학년도 9월 모평 1번을 풀어보도록 하자.
우리가 수학이란 것을 원칙에 따라 올바르게 접근을 하기 위해서는 먼저 우리가 알고 있는 정의를 사용할 수 있는지, 이를 사용하는 데 제약은 없는지 반드시 확인을 하는 습관을 들여야 한다. 그것이 정말 사소한 것일지라도 말이다.
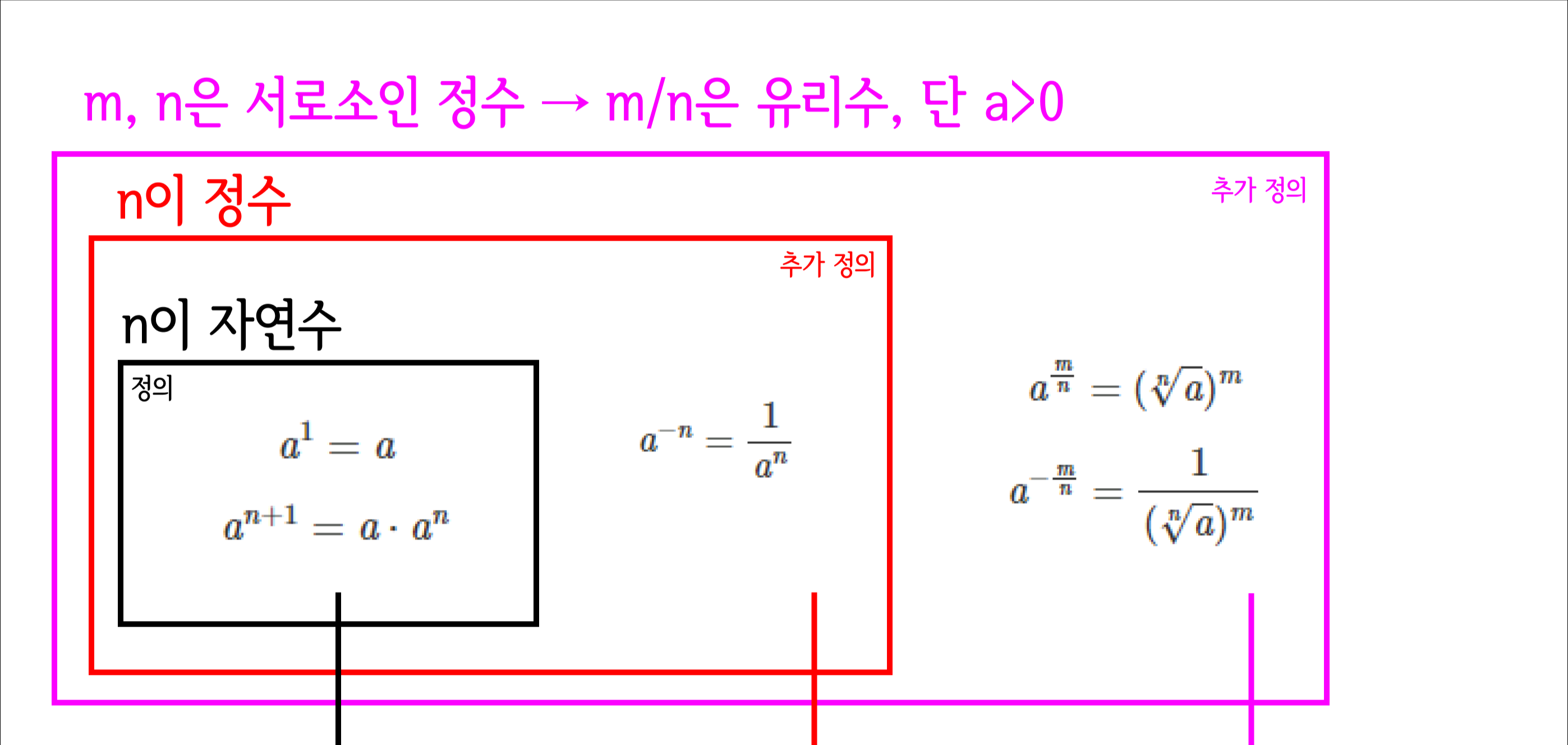
잘 보면, 유리수에서 정의를 하기 위해서 우리는 반드시 a>0임을 살펴야 한다. 문제에서 m제곱근, m루트 형태를 띄는 수들이 양수인지부터 확인해보면
$$ \sqrt[4]{32} \Rightarrow 32 > 0 $$
$$ \sqrt[8]{4} \Rightarrow 4 > 0 $$
즉, 모두 양수이므로, 지금까지 살펴보았던 정의들을 모두 사용할 수 있다. 어느정도 학습이 된 자들에게는 이러한 사실이 너무나도 당연한 것처럼 받아들여지겠지만, 이러한 전제를 한번이라도 짚어보고 넘어가는 습관은 장담하건데, 등급을 바꾸게 된다.
유리수에서의 지수를 정의할 수 있게 되었으니, 32의 4제곱근을 a, 4의 8제곱근을 b라고 놓자.
$$ \frac{\sqrt[4]{32}}{\sqrt[8]{4}} = \frac{a}{b} $$
이므로 우리는 a/b를 구하면 된다.
먼저 분자부터 살펴보면,
$$ \sqrt[4]{32} = a \quad \Rightarrow \quad a \times a \times a \times a = 32 \cdots (1)$$
같은 방식으로 분모는
$$ \sqrt[8]{4} = b \quad \Rightarrow \quad \overbrace{b \times b \times \cdots \times b}^{8개} = 4 $$
이때 4는 2×2 임을 이용하여 4개씩 아래와 같이 묶어보면
$$ \overbrace{b \times b \times b \times b}^{4개} \times \overbrace{ b \times b \times b \times b}^{4개} = 2 \times 2 $$
$$ b \times b \times b \times b = 2 \cdots (2) $$
(1)을 (2)로 나누면
$$ \frac{a \times a \times a \times a}{b \times b \times b \times b} = \frac{32}{2} = 16 = 2^4 $$
분수의 곱셈은 중학 과정에서 배우니
$$ \frac{a \times a \times a \times a}{b \times b \times b \times b} = (\frac{a}{b}) \times (\frac{a}{b}) \times (\frac{a}{b}) \times (\frac{a}{b}) = (\frac{a}{b})^4 $$
임은 알 수 있다. 결국
$$ (\frac{a}{b})^4 = 2^4 \quad \Rightarrow \quad \frac{a}{b} = 2 \quad(a, b>0 이므로) $$
즉, 우리가 구하고자 했던 a/b는 2임을 알 수 있다. 따라서 답은 ②
┃지수법칙을 이용하여 문제를 풀어보자
위의 방법은 중학과정에서 배우는 지수의 정의가 자연수임을 이용해서 정수, 유리수까지 확장시킨 뒤 그 정의를 활용하여 지수법칙을 이용하지 않고 푸는 방법에 대해서 알아본 것이다. 엄밀히 따져서 우리는 지수의 유리수 확장까지는 살펴보았지만 그 결과로 지수법칙이 모두 성립하는지 여부까지는 살펴보지 않았기 때문이다.
실제로 지수의 정의를 정수로 확장시켰다면, 자연수에서 성립하던 지수법칙이 정수에서도 성립하는지를 살펴야 한다.
$$ a^n \times a^m = a^{n+m} \cdots (1)$$
$$ (a^n)^m = a^{nm} \cdots (2)$$
$$ (ab)^n = a^n \times b^n \cdots (3)$$
$$ (\frac{a}{b})^n = \frac{a^n}{b^n} \cdots (4)$$
위의 대표적인 지수법칙 4개가
$$ n이\; 자연수 \;\Rightarrow\; n이\; 정수 (단, a^{-n} = \frac{1}{a^n}) $$
위의 조건에서도 성립하는지를 살폈어야 한다는 이야기. 정수에서 정의할 수 있는지와 위의 지수법칙이 정수에서도 성립하느냐는 완전히 다른이야기이기 때문이다.
다만 정수로 정의를 확장한 뒤로는 사실 증명하는 것 자체가 어려운 편은 아니므로, 이는 생략하고 기본적으로 지수가 정수, 유리수로 확장됐다면, 위의 지수법칙도 정수, 유리수에서도 성립한다는 것을 전제하여, 이번에는 지수법칙을 활용하여 문제를 쉽게 풀어보도록 하자.
지수법칙을 쓰는 경우에도 마찬가지로 지수가 유리수로 정의할 때는 똑같이 적용되는 전제조건! 바로 루트 a에서 a는 양수여야 한다는 것. 그러므로 이번에도 마찬가지로 루트안의 숫자들인 32, 4가 모두 양수라는 것을 반드시 짚어보고 가는 습관을 들여야 한다.
이제부터 문제에서 주어진 수를 지수법칙을 이용하여 풀면서 각 과정에서 어떤 법칙을 사용했는지 확인해보자.
\begin{alignat}{2} \frac{\sqrt[4]{32}}{\sqrt[8]{4}} & {} = \frac{32^{\frac{1}{4}}}{4^{\frac{1}{8}}} & \qquad & {} \cdots 제곱근의 \; 정의\\ \\ & {} = \frac{(2^5)^{\frac{1}{4}}}{(2^2)^{\frac{1}{8}}} & & {} \\ \\ & {} = \frac{2^{5 \cdot \frac{1}{4}}}{2^{2 \cdot \frac{1}{8}}} = \frac{2^{\frac{5}{4}}}{2^{\frac{1}{4}}} & \qquad & {} \cdots (2)법칙 \\ \\ & {} = 2^{\frac{5}{4}} \times \frac{1}{2^{\frac{1}{4}}} = 2^{\frac{5}{4}} \times 2^{- \frac{1}{4}} & \qquad & {} \cdots 정수지수의 \; 정의 \\ \\ & {} = 2^{\frac{5}{4} - \frac{1}{4}} & \qquad & {} \cdots (1)법칙 \\ \\ & {} = 2^{\frac{4}{4}} = 2^1 = 2 & & {} ■ \end{alignat}
풀어써서 그럴 뿐, 당연히 지수법칙을 이용해서 풀어내는 것이 몇 배는 더 간편하고 빠르다. 하지만 우리가 수학을 접근할 때, 문제를 풀어낼 때는 "내가 지금 계산한 이 간단한 과정이, 엄밀하게 사용해도 문제가 없는 과정인가?"라는 고민을 끊임없이 해야 한다.
정말 지수의 확장을 이 포스팅을 통해서만 확인한 사람이라면, 지수법칙으로 문제를 풀었을 경우 "당연히 지수법칙이 성립하겠지"라는 예단으로 문제를 접근한 것이 되므로, 올바른 방법이 아닐 수도 있다. 지금이야 아주 간단한 문제라서 그렇지 나중에 복잡한 정리를 사용하게 될 경우에는 이런 의문을 갖는다는 것 자체가 얼마나 자신의 수학실력을 높이는데 큰 힘이 되는지 깨닫게 될 것이다.
'수학 이야기' 카테고리의 다른 글
| 중학생이 풀어보는 수능 수학 - 2025학년도 대학수학능력시험 수학영역 2번, 함수와 수열이란? (1) | 2024.11.17 |
|---|---|
| 중학생이 풀어보는 수능 수학 - 2025학년도 대학수학능력시험 수학영역 1번 문제 풀이 (2) | 2024.11.15 |
| 중학생이 풀어보는 수능 수학 - 2025학년도 9월 모평 1번 문제, 제곱근의 개념과 지수의 확장(정수 → 유리수) (3) | 2024.11.10 |
| 지수법칙의 확장(자연수 → 정수), 지수법칙을 정수로 확장시키기 위해서 만든 약속 (0) | 2024.11.07 |
| 중학생이 풀어보는 수능 수학 - 2025학년도 9월 모평 1번 문제, 거듭제곱의 개념 (0) | 2024.11.05 |

