2025학년도 대학수학능력시험 수학영역 6번 (2025. 11. 14.)

이전 글에서 이어지는 내용입니다.
2025.04.08 - [수학 이야기] - 중학생이 풀어보는 수능 수학 - 2025학년도 대학수학능력시험 수학영역 6번, 호도법과 라디안, 호도법(라디안을 쓰는 이유)
중학생이 풀어보는 수능 수학 - 2025학년도 대학수학능력시험 수학영역 6번, 호도법과 라디안, 호
2025학년도 대학수학능력시험 수학영역 6번 (2025. 11. 14.) 이전 글2025.03.03 - [수학 이야기] - 중학생이 풀어보는 수능 수학 - 2025학년도 대학수학능력시험 수학영역 6번, 피타고라스 정리와 삼각비,
wkqtkdtlr.tistory.com
sin과 cos
호도법까지 모두 알아보았으니 이제 본격적으로 삼각비에 대해서 알아보자.
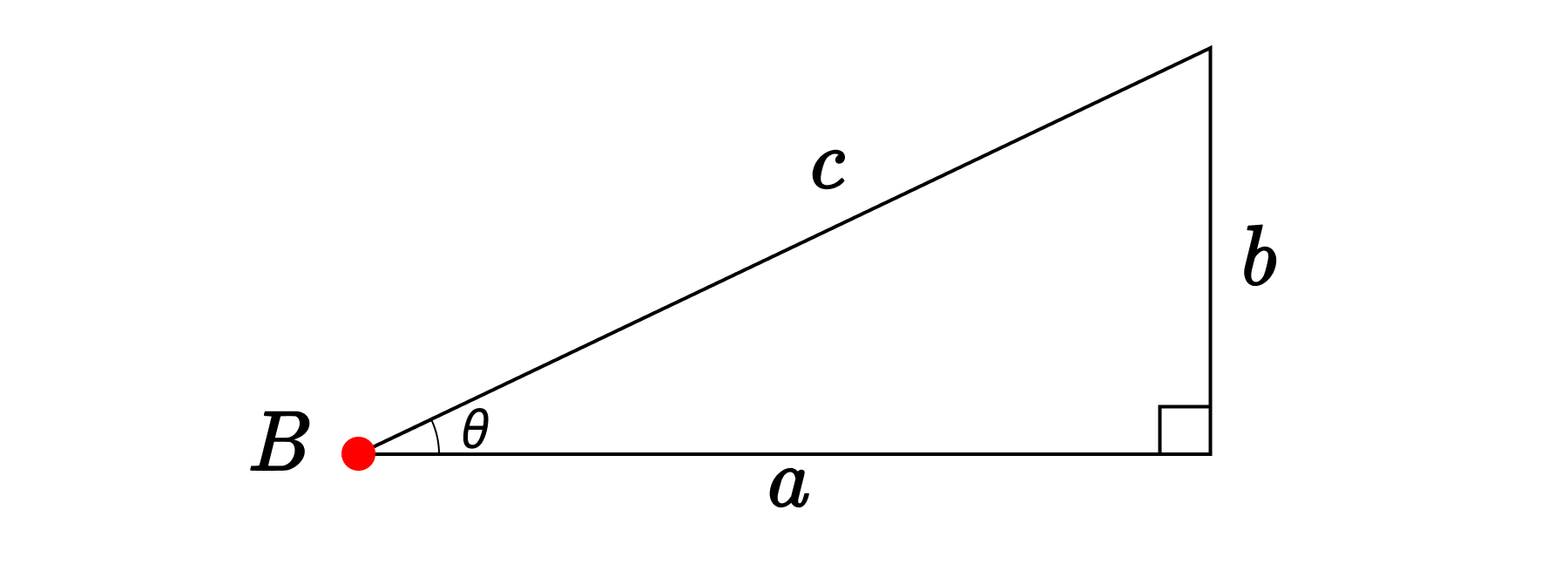
다음과 같은 삼각형이 있고 ∠B의 각을 $\theta$라고 해보자. 우리는 지난 포스팅을 통해 직각삼각형에서 직각을 제외한 한 각을 고정시킨 모든 삼각형들은 닮음이고, 닮은 삼각형끼리는 두 변의 관계가 항상 같음을 알고 있다. 즉, 빗변 $c$를 기준으로 $\angle{B} = \theta$인 직각삼각형은 그 삼각형의 크기와 상관없이 $\dfrac{a}{c}, \, \dfrac{b}{c}$는 항상 일정하다. 이건 수학적으로 무슨 의미를 갖는 것일까?
$\frac{b}{c}$의 값은, ∠B의 크기만 같다면, $b, \, c$가 어떻게 변하더라도 항상 같다는 의미이고, 이는 곧, $\frac{b}{c}$가 $\theta$에 의해서만 그 값이 결정된다는 것을 의미한다. 여기서, $\theta$를 우리가 자주 쓰는 $x$, $\frac{b}{c}$를 $y$라고 생각해보자.
"$x$의 값에 따라 $y$이 결정된다."
어디에서 많이 본 형태가 아닌가? 바로 $f(x) = y$인 함수랑 똑같지 않나? 즉, $\theta$를 변수로 갖는 함수로 표현이 가능하다는 것이다.
$$f(\theta) = \frac{b}{c}, \quad (\angle{C} = \frac{\pi}{2}, \, 0 < \theta < \frac{\pi}{2} ) $$
같은 이유로 $\dfrac{a}{c}$도 똑같이 표현할 수 있다.
$$g(\theta) = \frac{a}{c}, \quad (\angle{C} = \frac{\pi}{2}, \, 0 < \theta < \frac{\pi}{2} )$$
앞으로 계속 쓰일 이 함수들을 항상 이와 같이 정의하면서 사용할 수 없으므로, 특별히 이 두 함수에 대해서는 $f(\theta) = \sin{\theta},\, g(\theta) = \cos{\theta}$로 이름을 붙혀주기로 한 것이 sin(사인), cos(코사인)의 시작이다.
$ 0 < \theta < \dfrac{\pi}{2} $에서 위 그림의 직각삼각형에 대해 sin, cos은 다음과 같이 정의한다.
$$\sin{\theta} = \frac{b}{c} $$
$$\cos{\theta} = \frac{a}{c} $$
반지름이 1인 원과 직각삼각형
먼저 위의 sin, cos에 대한 정의를 이용해 다음과 같이 바꿔 표현해보자.
$$c \sin{\theta} = b, \quad c \cos{\theta} = a $$
그리고, 기저(basis)를 설명하면서 봤던 반지름이 1인 원(이전 포스팅 참고)과 직각삼각형의 관계를 생각하며 아래 그림을 살펴보자
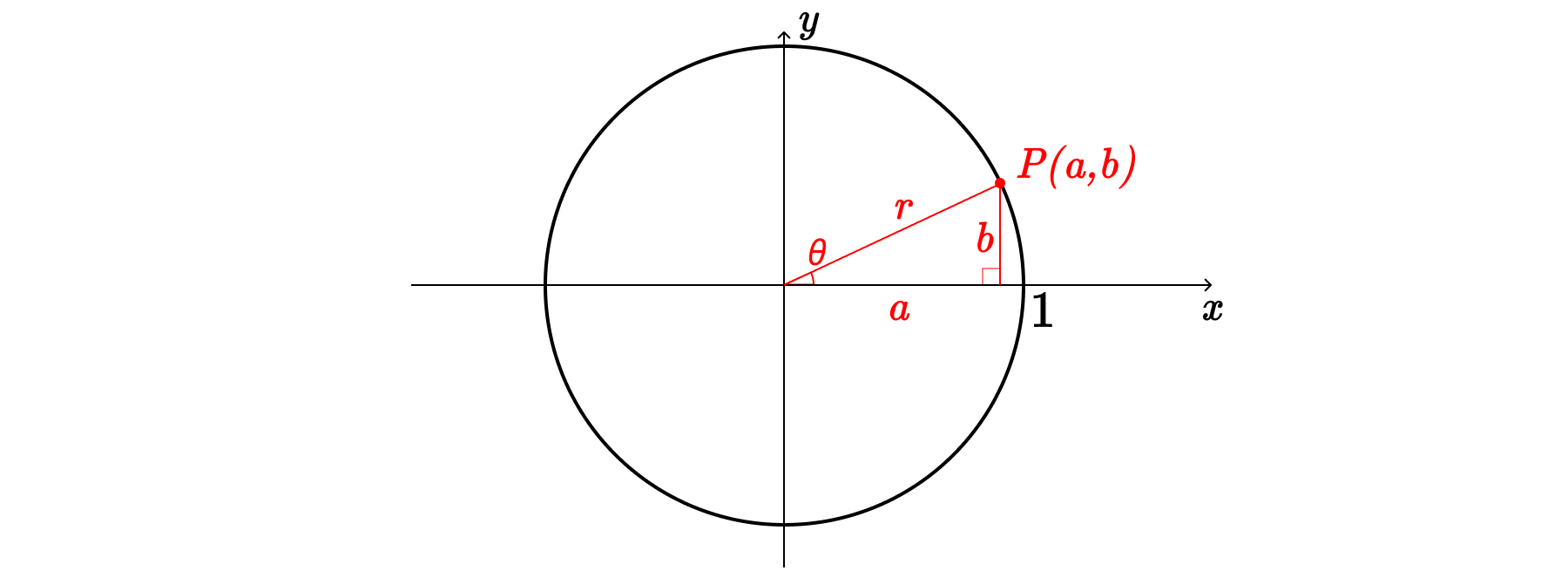
원 위의 점 P에 대해서, $x$축과 수직을 이루도록 선을 하나 그으면, 위의 빨간색으로 보이는 직각삼각형이 하나 만들어진다. 이 직각삼각형을 맨 위에 그려놓은 직각삼각형과 비교해보면, 빗변 $c$가 원의 반지름인 $r$로 바뀌었을 뿐이다. 따라서, c → r로 바꾸어 다음과 같이도 표현할 수 있다.
$$ r \cos{\theta} = a, \,\, r \sin{\theta} = b $$
이 때, 이 원의 반지름 $r=1$이므로, $a = \cos{\theta}, \, b = \sin{\theta}$가 된다. 결국, 반지름이 1인 원 위의 점 P는 다음과 같이 표현할 수 있다.
$$P(a, \, b) = P (\cos{\theta}, \, \sin{\theta}) $$
결국, 반지름이 1인 원 위의 점은 어떤 점을 선택하더라도 그 좌표를 sin, cos으로 바꾸어 표현하는 것이 가능하다. 하지만, 우리는 이것이 직각삼각형임을 잊지 않아야 한다. 즉, 이러한 표현은 $0<\theta<\dfrac{\pi}{2}$에서만 정의할 수 있는 표현이다.
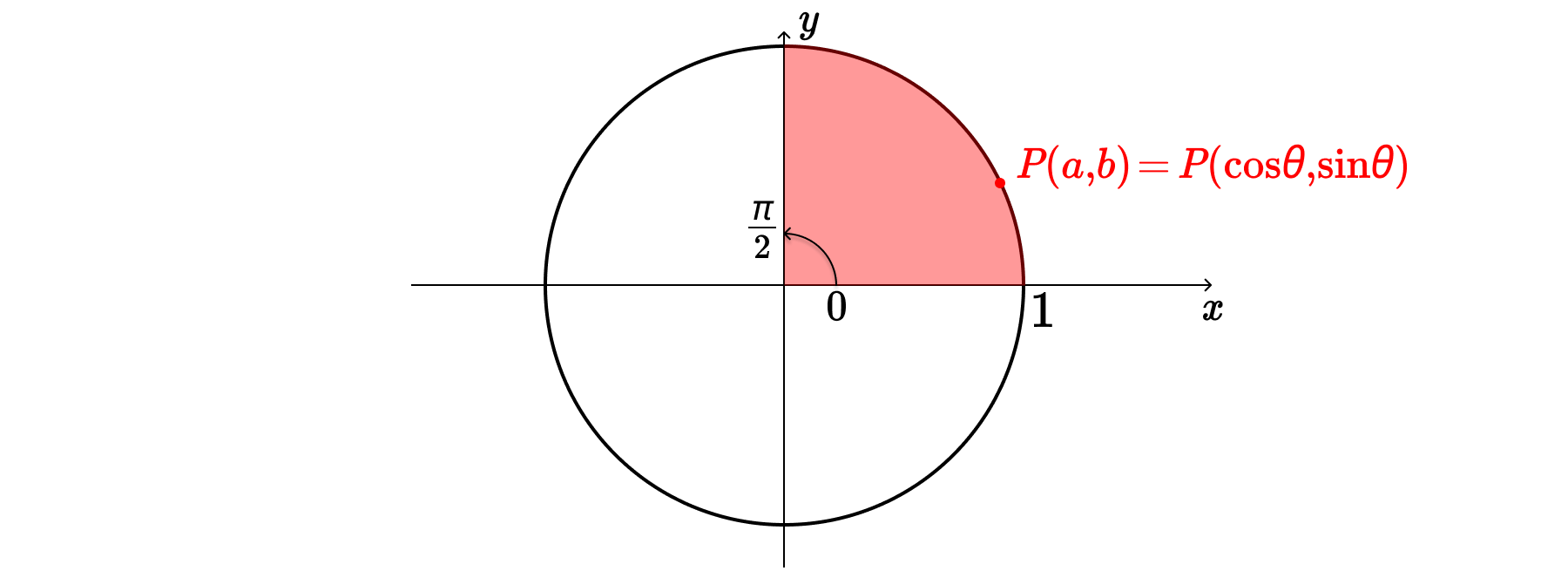
그렇다면, 어차피 좌표값을 sin, cos으로 표현해봤으니, 직각삼각형이라고 생각하지 말고 그냥 이 원 위에 있는 점의 $x$좌표를 $\cos{\theta}$, $y$좌표를 $\sin{\theta}$라고 정의해도 괜찮은 것이 아닐까? 그렇게 한다면, 직각삼각형에서 벗어날 수 있으니 θ가 $\dfrac{\pi}{2}$를 넘어도 표현할 수 있게 되는 것 아닐까? 삼각함수는 바로 이러한 생각에서 시작하게 된다.
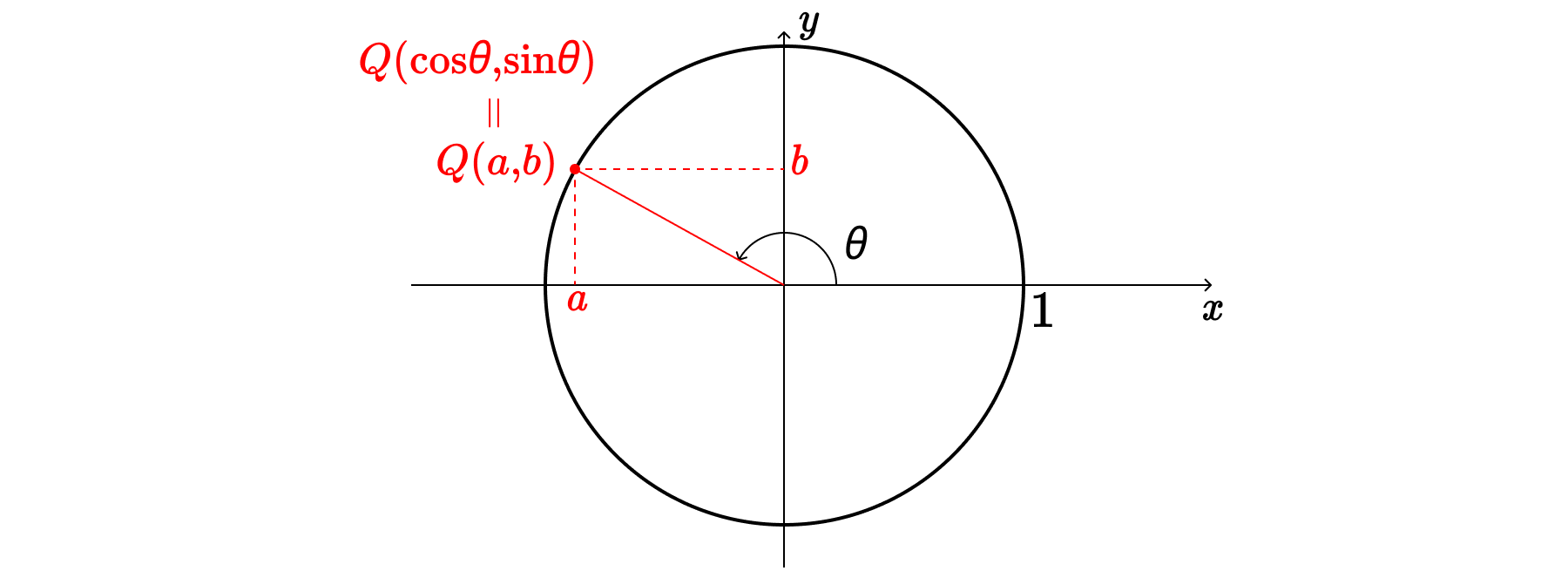
위와 같이, 임의의 원 위의 점 Q에 대해, Q와 원점 O를 잇는 $\overline{QO}$와 양의 $x$축이 이루는 각을 θ라고 할 때, 점 Q의 $x$좌표 $a$를 $\cos{\theta}$로 정의해버리자는 것이다. 이렇게 정의하면, 위 그림의 경우에는 $a<0$이기 때문에 $\cos{\theta} < 0$이 된다. 직각삼각형에서 sin, cos의 정의는 "길이의 비"를 나타내는 함수였기 때문에, 그 값이 무조건 양수일 수 밖에 없었지만, $x$좌표를 나타내는 값으로 바꾸니 cos값이 음수가 나올 수도 있게 된다.
다시 말해, $x$좌표의 값이 음수가 되는 2사분면, 3사분면 위의 점에 대해서는 cos값이 음수가 나온다는 것이다.

같은 원리로, $y$좌표의 값을 나타내는 sin값은 3사분면, 4사분면에서 음수가 나올 수 있게 된다.

이렇게 삼각함수로 개념을 확장시켰더니, 절대 삼각비로는 정의할 수 없었던 것들이 재정의되고 있다. 예전에 살펴보았던 지수법칙이 확장되는 것과 같이 말이다.
반지름이 1이 아니더라도 같다
그렇다면, 이제는 반지름이 1인 원이 아닌 일반적인 반지름 r에 대해서도 이를 설명해보자(일반화)

반지름이 r인 원 위의 점도 결국 똑같이 설명할 수 있다. 지금까지 살펴 본 반지름이 1인 원에서 빗변의 길이가 r로 비례하여 변했을 뿐이다. 파란색 삼각형과 빨간색 삼각형은 그 끼인각이 같은 닮은 삼각형이므로 모든 길이의 비가 빗변의 길이의 비인 $1:r$로 같다. 따라서 $x$좌표, $y$좌표 역시 똑같이 $r$배 변하여 $Q(r\cos{\theta}, \, r\sin{\theta})$가 된다.

지금까지 살펴 본 내용을 다시 정리해보자. 임의의 2차원 평면 위의 점 P에 대해서 P와 원점 O와의 거리를 $r$, $\overline{OP}$와 양의 $x$축이 이루는 각을 $\theta$라고 하면, 반드시 다음을 성립하게 된다.
$$P(a, b) = P(r\cos{\theta}, r\sin{\theta}) $$
이렇게 평면위의 점을 $r, \, \theta$로 표현하는 것을 "극좌표계"라고 한다.
그럼 지금까지 내용을 토대로 위의 문제를 풀어보자.
문제에 제시된 바와 같이,
$$ \cos{(\frac{\pi}{2} + \theta)} = - \frac{1}{5} \quad \cdots (1) $$
를 만족하는 점 P가 있다고 해보자. P의 $x$좌표 값인 cos의 값이 음수로 나왔으므로, 위에서 살펴 본 바와 같이 점 P는 2사분면, 3사분면 사이에 있게 된다.

(그림에서는 점 P를 3사분면에 놓았지만, 2사분면 위에 있어도 상관이 없다)
따라서, 중심각으로 표현된 $(\dfrac{\pi}{2} + \theta)$의 범위는 다음과 같다.
$$ \frac{\pi}{2} < \frac{\pi}{2} + \theta < \frac{3}{2} \pi $$
정리하면,
$$ 0 < \theta < \pi $$
로 1, 2사분면의 범위를 갖는다.
즉, $P(\cos{(\dfrac{\pi}{2} + \theta)}, \, \sin{(\dfrac{\pi}{2} + \theta)})$는 2, 3사분면에 있는 점이지만, 새롭게 정의하는 점 $Q(\cos{\theta}, \, \sin{\theta})$는 1, 2사분면 위의 점이 된다.
이 때, 위의 (1)번 조건식을 조금 변형하면,
$$ 5 \cos{(\frac{\pi}{2} + \theta)} = -1 $$
즉, 원점과의 거리가 5이면서 $x$좌표의 값이 -1인 점이 된다. 이런 점은 딱 2개 존재하는데,
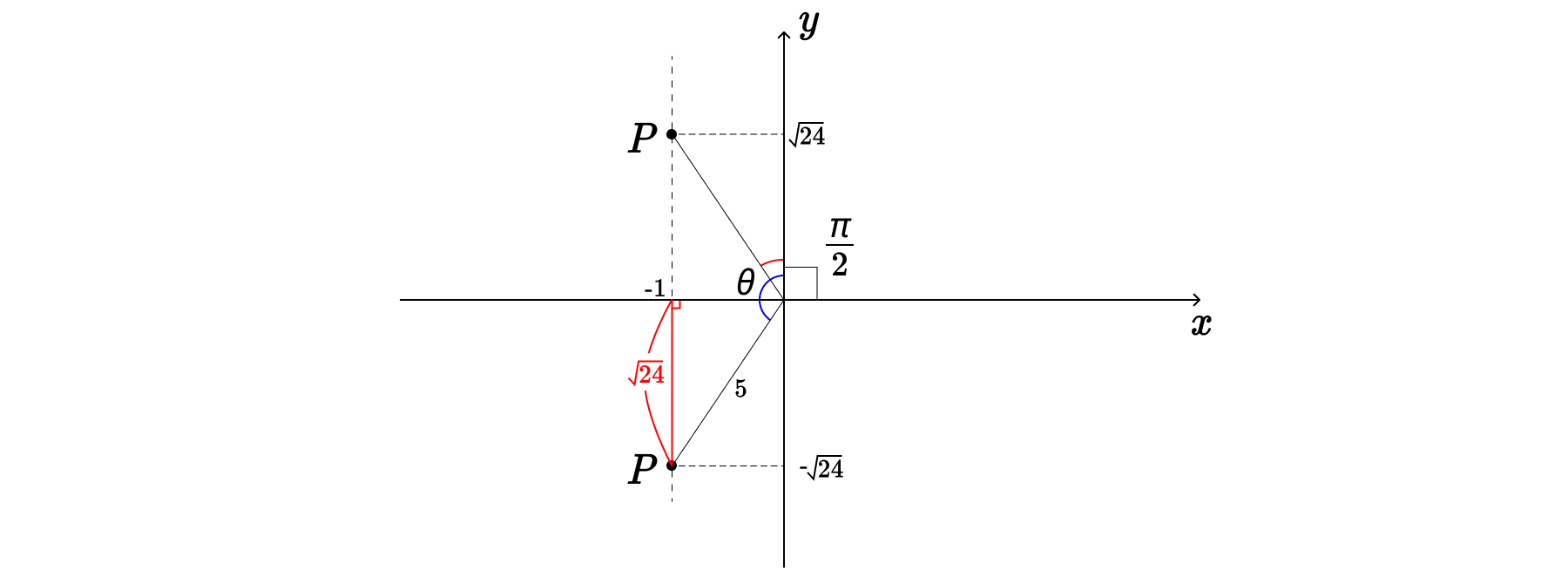
$\theta$가 빨간색일지, 파란색일지는 알 수 없다. 어찌됐든 피타고라스의 정리로 높이가 $\sqrt{24}$는 것은 알 수 있으므로, 점 P는 $(-1, \, \sqrt{24})$이거나, $(-1, \, - \sqrt{24})$ 이다.
우리가 구해야 하는 것은 $\dfrac{\sin{\theta}}{1 - \cos^2{\theta}}$이므로, $\theta$에 대한 sin, cos 값이 필요하다. cos, sin 값은 양의 $x$축과 이루는 각을 기준으로 정의하고 있는데, 지금 위의 그림에서 $\theta$는 양의 $y$축과 이루는 각이다. 우리가 구하고 싶은 값은 $\cos{(\frac{\pi}{2} + \theta)}$가 아니라 $\cos{\theta}$이므로, 이것을 한번 90도 시계방향으로 회전시켜서 $\theta$가 $x$축과 이루는 각이 되도록 만들자

$\theta$를 양의 $x$축과 이루는 각이 되도록 만들었으므로, 점 P를 회전시켜 만든 새로운 점 Q는 이제 $sin{\theta}, \, \cos{\theta}$로 표현이 가능해졌다. 즉, 새로운 점 Q는 $(5 \cos{\theta}, \, 5 \sin{\theta})$으로, 오른쪽 그림에 따라 $(-\sqrt{24}, 1)$ 이거나 $(\sqrt{24}, 1)$이 된다. 정리하면
$$ \cos{\theta} = \frac{\sqrt{24}}{5} \; or \; - \frac{\sqrt{24}}{5}$$
$$ \sin{\theta} = \frac{1}{5}$$
가 된다. Q가 1, 2사분면에 있는 점이므로, 위에서 살펴본 바와 같이 sin값은 무조건 양수가 될 수 밖에 없기도 하다. 문제는 cos의 값이 양수가 되기도 하고 음수가 되기도 한다는 점인데 다행히 문제에서는 $\cos^2{\theta}$를 원하므로
$$ \cos^2{\theta} = \frac{24}{25} $$
로 항상 일정하게 된다. 따라서, 우리가 구하고자 하는 값은
$$\begin{align} \frac{\sin{\theta}}{1-\cos^2{\theta}} & = \frac{\dfrac{1}{5}}{1 - \dfrac{24}{25}} \\ \\ & = \frac{\dfrac{1}{5}}{\dfrac{1}{25}} \\ \\ & = 5 \end{align} $$
따라서 답은 ⑤이 된다.



