2025학년도 대학수학능력시험 수학영역 6번 (2025. 11. 14.)

이전 글
2025.02.20 - [수학 이야기] - 중학생이 풀어보는 수능 수학 - 2025학년도 대학수학능력시험 수학영역 6번, 삼각형의 닮음 조건은 이유가 없나? 삼각형의 닮음 증명
중학생이 풀어보는 수능 수학 - 2025학년도 대학수학능력시험 수학영역 6번, 삼각형의 닮음 조건
2025학년도 대학수학능력시험 수학영역 6번 (2025. 11. 14.)처음으로 기하파트의 문제가 나왔다. 사실 삼각함수는 대수에 가까운가, 기하에 가까운가에 대한 이야기는 다를 수 있지만, 적어도 교육과
wkqtkdtlr.tistory.com
삼각비란 무엇인가
그럼 이제 우리가 지난 포스팅을 통해 삼각형의 닮음을 주구장창 이야기했던 이유에 대해서 알아보자. 삼각형의 닮음은 여러 방식으로 정의할 수 있지만, 우리가 필요로 하는 정의는 다음의 하나이다.
삼각형이 닮음이다 ⇔ 세 쌍의 변의 길이의 비가 같다
길이의 비가 같다는 것은 무엇을 의미할까? 아래의 그림을 살펴보자

이 두 삼각형은 서로 닮았다. 닮았다는 것은 세 쌍(여기에서 세 쌍은 $a, \, a'$, $b, \, b'$, $c, \, c'$)의 길이의 비가 같다는 것이므로 다음과 같이 표현할 수 있다.
$$ a:a' = b:b' = c:c' $$
비(比) 라는 것은 수학에서는 곱셈이라고 생각하면 편하다. a와 a'의 비 = k라는 의미는, a에 k를 곱하면 a'이 된다는 이야기이며, a, a'과 b, b'의 비가 서로 같다는 말은 a가 a'이 되려면 k를 곱할 때, 같은 값 k를 b와 곱하면 b'가 된다는 것을 의미한다. 수식으로 표현하자면
$$ \frac{a}{a'} = \frac{b}{b'} = \frac{c}{c'} = k \quad (k \in \mathbb{R}) $$
이 된다. 그럼 a와 b의 관계만 살펴보면,
$$ \begin{align} & \quad \frac{a}{a'} = \frac{b}{b'} \\ \\ \Leftrightarrow & \quad a \cdot b' = b \cdot a' \\ \\ \Leftrightarrow & \quad \frac{a}{b} = \frac{a'}{b'} = k \quad (a, \, b \neq 0) \end{align} $$
이건 무엇을 의미하는 것일까?

바로, 두 삼각형이 닮았다면, 같은 쌍의 길이의 비가 같기도 하지만, 한 삼각형에서 두 변(a, b)의 관계가 닮은 삼각형(a', b')에도 그대로 유지된다는 것을 의미한다. 쉽게 말해서, 왼쪽의 삼각형과 닮은 모든 삼각형은 a에 대응되는 변과 b에 대응되는 변의 길이의 비가 $k$로 항상 일정하다는 것을 보여준다.($ \dfrac{a}{b} = k $)
그렇다면 하나의 삼각형에서 길이의 비는 총 3개가 나온다. 관계를 정의하기 위해선 2개의 변이 필요한데, 3개의 변 중에서 2개의 변을 고르는 방법은 (a, b), (b, c), (a, c) 뿐이기 때문이다. 즉, 삼각형에서 길이의 비란, 하나의 끼인각을 두고 양 옆의 변끼리 관계, 수만가지 닮은 삼각형을 두더라도 위와 같은 끼인각을 중심으로 하는 두 변의 길이의 비는 단 하나의 수로 정의할 수 있다는 것이다. 이를 우리는 끼인각을 3개 가지고 있어 "삼각비"라고 부른다.
피타고라스 정리의 의미
즉, 삼각비란, 삼각형에서 두 변의 길이의 비를 표현하는 말이다. 그런데, 중학교 과정에서 "피타고라스 정리 → 삼각비의 정의" 순서로, 특별한 삼각형인 "직각"삼각형에 대해서 이를 학습하고 있다. 많고 많은 삼각형 중 왜 직각삼각형일까? 그 답은 피타고라스 정리에 있다.

다음과 같은 직각삼각형이 있다면, 각각의 빗변의 길이에 대해서 다음과 같은 식이 반드시 성립한다
$$ a^2 + b^2 = c^2 $$
이를 피타고라스 정리라고 부르는데, 이 정리가 갖고 있는 특별함은 바로 직각삼각형에서는 "언제나" 성립한다는 것이다. 다르게 표현하면 "직각삼각형에서 두 변의 길이를 알면, 나머지 한 변의 길이는 무조건 계산할 수 있다."라는 것을 의미한다. 아래의 예제를 살펴보자

위의 직각삼각형들은 모두 두 변의 길이가 주어져 있다. 이를 통해 나머지 한 변의 길이인 $x, \, y$를 구해보자.
(왼쪽)
$$ \begin{align} & 3^2 + 4^2 = x^2 \\ \\ \Rightarrow \quad & 9 + 16 = 25 = x^2 \\ \\ \Rightarrow \quad & x=5 \quad (\because x >0) \end{align} $$
(오른쪽)
$$ \begin{align} & 5^2 + y^2 = 13^2 \\ \\ \Rightarrow \quad & 25 + y^2 = 169 \\ \\ \Rightarrow \quad & y^2 = 144 \\ \\ \Rightarrow \quad & y = 12 \quad (\because y > 0 ) \end{align} $$
이와 같이 피타고라스 정리를 이용하면, 두 변의 길이만으로도 남은 한 변의 길이를 구할 수 있게 된다.
직각삼각형에서는 직각이 아닌 다른 하나의 내각이 중요하다
이쯤에서 다시 삼각비의 의미를 살펴보자. 위에서 빨간색 부분으로 표시한 부분만 빼보면
"삼각형이 닮았다 ⇒ 두 변의 관계는 그대로 유지된다 = 두 변의 관계는 항상 일정하다, 같다." … (1)
그리고 이전 포스팅에서 살펴본 삼각형의 닮음 조건 중
"삼각형의 세 각의 크기가 같다 ⇒ 그 삼각형들은 모두 닮음이다"
그런데, 우리가 지금 살펴보고 있는 "직각삼각형"은 이미 한 개의 각이 직각인 90º이다. 그렇다면, 사실상 직각삼각형에서 직각이 아닌 다른 끼인각을 알고 있다면, 삼각형의 세 각의 크기를 알고 있는 것과 같다. 아래 그림을 살펴보자
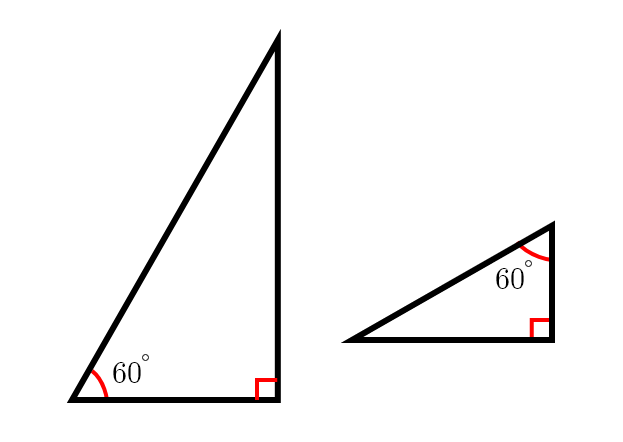
이 두 삼각형은 서로 닮음일까? 삼각형의 내각의 합은 180º이므로, 지금 표시되지 않은 나머지 한 각은 두 삼각형 모두 30º로 같다. 그렇다면, 세 각의 크기가 모두 같기 때문에, 이 두 삼각형은 닮았다고 할 수 있겠다. 즉, 우리는 "직각삼각형"이라는 특수한 삼각형에서 만큼은 직각을 제외한 단 하나의 내각만 같아도 모두 닮았다고 할 수 있다
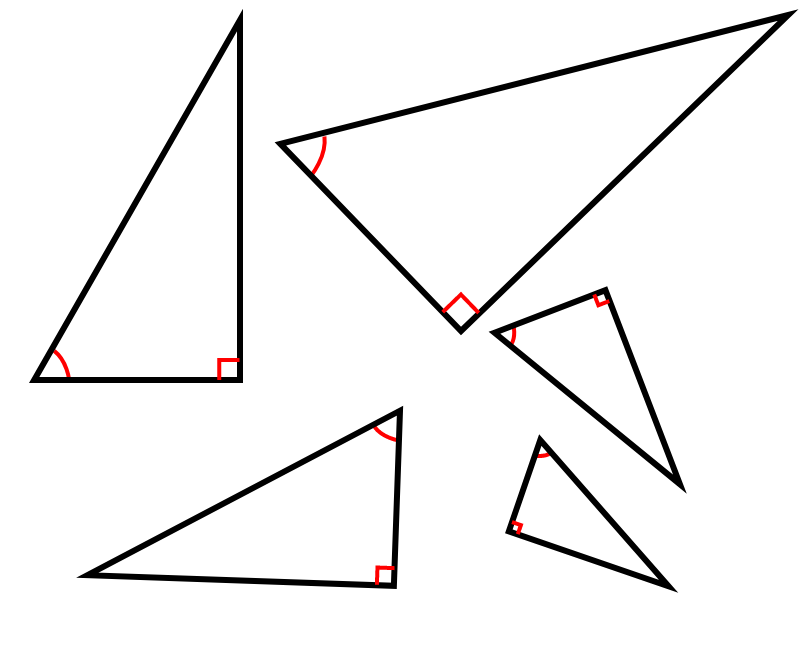
따라서, 위와 같이 직각삼각형에서 직각이 아닌 다른 하나의 내각이 같다는 정보만 있다면, 그 삼각형들은 모두 닮음이라는 것을 의미한다.
"직각삼각형에서 직각이 아닌 나머지 내각 중 하나가 같다 ⇒ 그 삼각형들은 모두 닮음이다" … (2)
결국, (1), (2)에 의해서
"직각삼각형에서 직각이 아닌 내각이 같다 ⇒ 해당 삼각형의 두 변의 관계, 두 변의 비율은 항상 일정하다"
위의 명제는 무엇을 의미하는 것일까?

그림과 같이 끼인각은 모르지만, 직각이 아닌 내각이 같다는 사실을 알고 있는 직각삼각형이 있다. 직각이 아닌 내각이 같으면, 두 변의 관계, 즉, 두 변의 비율은 항상 일정하기 때문에
$$ \begin{align} & \frac{8}{4\sqrt{3}} = \frac{x}{12} \\ \\ \Rightarrow \quad & x = 8\sqrt{3} \end{align} $$
로 $x$를 구할 수 있게 된다.
"각이 같다면 비율은 일정하다.", 이 단순한 문장 하나를 고대수학자들은 다른 방식으로 접근하기 시작한다. "그렇다면, 각에 따른 변의 비율을 미리 외우고 있으면, 한 변의 길이만 알아도, 나머지 변의 길이를 알 수 있지 않을까?"라고...
삼각비의 탄생
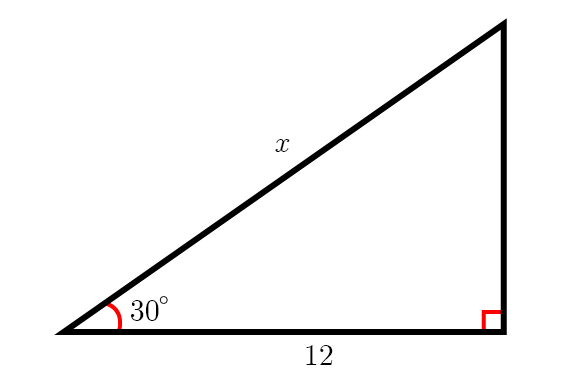
고대 수학자들은 직각삼각형의 한 내각에 따른 두 변의 비율을 미리 계산해두기 시작한다. 직각이 아닌 한 내각이 30º, 이를 끼고 있는 두 변인 빗변과 한 밑변의 비율은 항상 $ \dfrac{\sqrt{3}}{2} $임을 알고있다면, 한 내각이 30º인 직각삼각형은 모두 닮음이기 때문에 빗변과 밑변의 비율은 항상 $ \dfrac{\sqrt{3}}{2} $이게 된다. 따라서
$$ \begin{align} & \frac{\sqrt{3}}{2} = \frac{12}{x} \\ \\ \Rightarrow \quad & x = 12 \cdot \frac{2}{\sqrt{3}} \\ \\ \Rightarrow \quad & x = 12 \cdot \frac{2\sqrt{3}}{3} \\ \\ \Rightarrow \quad & x = 8\sqrt{3} \end{align} $$
그렇다면, 피타고라스의 정리에 의해 직각삼각형의 높이($h$)는 다음과 같이 구할 수 있다.
$$ \begin{align} & 12^2 + h^2 = (8\sqrt{3})^2 \\ \\ \Rightarrow \quad & h^2 = 192 - 144 = 48 \\ \\ \Rightarrow \quad & h = 4\sqrt{3} \quad (\because h > 0) \end{align} $$
즉, 직각삼각형에서 직각이 아닌 내각의 크기와 한 변의 길이만 알고 있다면, 직각삼각형 세 변의 길이를 모두 알 수 있게 된다.

서울에서 대전까지의 직선거리는 약 143km이다. 대전 - 서울 - 원주 지역이 이루는 각도가 57º정도 된다는 사실을 알고 있다면, 서울에서 원주까지의 거리는 어떻게 될까? 57º일 때 빗변과 밑변의 비율을 모르기 때문에 알 수 없을까? 아니다. 모르면, 직접 종이에 한 내각이 57º인 직각삼각형을 그려보면 된다. 직각이 아닌 내각이 같다면, 그 비율은 언제나 같기 때문이다.
내각이 57º인 직각삼각형의 밑변 / 빗변의 비율은 약 0.5446정도가 된다. 따라서 서울에서 원주까지의 거리는
$$ 143 \times 0.5446 = 77.9 $$
이다. 물론 피타고라스 정리를 이용하면 대전 - 원주간 거리도 구할 수 있게 된다.

직각삼각형을 그리기 위한 거리, 실제 대전 - 서울 - 원주가 이루는 각도의 오차 등을 생각하면, 7km정도의 오차는 너무나 사소한 수준이다. 오히려 꽤나 정확하게 구했다고 생각해도 된다. 즉, 조선시대라도 서울에서 대전까지의 거리만 정확하게 잴 수 있었다고 하면, 천문 등을 통해 다른 도시들과 서울 - 대전이 이루는 각을 구하여 굳이 직접 가보면서 측정하지 않아도 꽤 높은 정확도로 서울에서 다른 지역까지의 거리를 구할 수 있었다. 비율을 굳이 외울 필요도 없다. 종이에 같은 내각의 직각삼각형을 그려서, 자로 재보면 되니까.
삼각비는 이렇게 하나의 거리와 하나의 내각만으로 직각삼각형의 모든 정보를 추론할 수 있게 해준다. 그렇게 삼각비는 탄생하게 된다.



