중학생이 풀어보는 수능 수학 - 2025학년도 대학수학능력시험 수학영역 6번, 호도법과 라디안, 호도법(라디안을 쓰는 이유)

728x90

2025학년도 대학수학능력시험 수학영역 6번 (2025. 11. 14.)

 

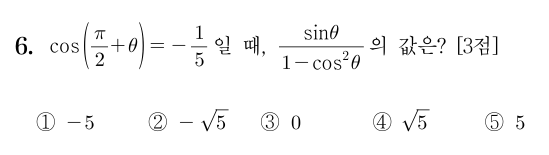
이전 글

2025.03.03 - [수학 이야기] - 중학생이 풀어보는 수능 수학 - 2025학년도 대학수학능력시험 수학영역 6번, 피타고라스 정리와 삼각비, 삼각형의 모든 정보를 담다

중학생이 풀어보는 수능 수학 - 2025학년도 대학수학능력시험 수학영역 6번, 피타고라스 정리와

---

기저, basis

여기 직경 30cm의 냄비 뚜껑이 있다고 가정해보자. 이 냄비 뚜껑은 후라이팬이든 냄비든 접시든 직경이 30cm인 것에는 모두 완벽하게 덮힐 것이다. 또한, 이 뚜껑을 일본으로 가지고 가든, 미국으로 가지고 가든 직경 30cm의 냄비에는 모두 정확하게 맞을 것이다. 우리는 당연히 그럴 것이라고 확신할 수 있다. 왜 그럴까?

 

그 이유는 전 세계가 1m의 정의를 모두 똑같이 하고 있기 때문이다. 과거에는 적도까지의 자오선 어쩌구 저쩌구, 지금은 빛이 3억분의 1초동안 이동한 거리 등등 미터를 정의하는 방법은 꾸준히 변해왔지만, 어찌됐든 전 세계가 같은 길이를 1m로 규정하고 이를 이용하여 길이를 재고 있기 때문에, 세계 어느 곳을 가더라도 1m는 항상 동일하다는 것이다. 

 

유클리드 공간 내에 (4, 3)이라고 정의된 한 점이 있다고 하자. 우리는 너무나도 당연하게, 원점에서 $x$축으로 4, $y$축으로 3만큼 이동한 점이라고 정의하고 있지만 사실 아주 모호한 표현 중 하나이기도 하다. $x$축에서 4만큼 이동한다는 것은 도대체 얼마만큼 이동한 것을 이야기하는 것일까? 지구상의 단위 4cm일까? 아니면 4m? 그것도 아니라면 4야드일까? 

 

하지만 우리는 유클리드 공간 내의 점을 표현할 때 (4, 3)이라고 표현하지 (4m, 3m)라고 단위를 붙히지 않는다. 지구상에서 무언가의 길이를 잴 때, "m"라는 "미터법"을 기준으로 한다는 것을 나타내는 것처럼, 유클리드 공간 내에서는 기저(基底, basis)라는 것을 기준으로 하는데, $x$축 방향으로 길이가 1인 기준(기저, 단위)을 $e_0$, $y$축 방향으로 길이가 1인 기준(기저, 단위)을 $e_1$이라고 하면, 원래 (4, 3)은 미터법과 같이 $(4e_0, \, 3e_1)$이라고 단위를 써야하지만, 보통 이를 생략하고 (4, 3)으로 표현하는 것이고, 우리는 이를 익숙하게 사용하는 것이다. 

 

본래 기저는 방향의 개념도 가지고 있기 때문에, 수학에서는 이를 "기저벡터"라고 표현하지만, 내가 여기서 하고자 하는 말은 기저의 의미 정도이지, 심화 개념을 짚고 가려는 것이 아니다. 그럼 기저를 왜 설명한 것일까? 내가 여기서 중요하게 다루고 싶은 내용은 바로 기저의 길이(크기)는 기본적으로 "1"이라는 것이다.

 

라디안의 개념

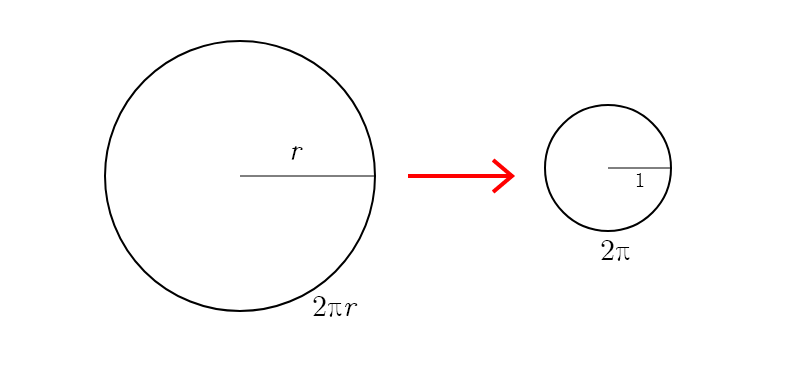
반지름이 $r$인 원의 둘레의 길이는 $2 \pi r$이다. 그럼 반지름의 길이가 1이라면 그 원의 둘레의 길이는? $r = 1$이므로 $2 \pi$이다. 

중심각의 크기가 45도인 호의 길이는 전체가 360도인 원에서 $\frac{45}{360} = \frac{1}{8}$만큼 차지하므로, 호의 길이도 원의 둘레 길이의 1/8이 된다. 즉, 중심각의 크기가 $\theta$인 호의 길이는 다음과 같이 나타낼 수 있다. 

 

호의 길이 $l = 2 \pi r \times \dfrac{\theta}{360} $

 

여기까지는 중등과정에서도 너무나 당연한 것이다. 하지만, 왜 우리가 앞서 기저라는 개념과, 반지름이 "1"인 원을 굳이 살펴보았을까? 아래의 그림을 자세히 들여다보자.

각도란 그 정의대로, 두 직선이 벌어진 정도를 나타내는 값이고, 위의 그림에서는 중심각이 $\theta$이다. 그런데, 이 각도라는 것은 위에 보이는 여러 색깔의 선 중 무엇을 말하는 것일까? 두 직선이 벌어진 정도는 검은색의 가장 작은 부분의 $\theta$나 빨간색, 더 나아가 딱 봐도 엄청 커 보이는 파란색 $\theta$도 모두 다 $\theta$라고 부른다. 물론 각도라는 것은 길이가 아니라 벌어진 "정도"이므로, 어떤 것을 고르더라도 그 각도가 변할 일은 없다.

 

하지만, 우리가 위에서 유클리드 공간에서 기저를 정해, 어떤 점이 원점으로부터 얼마나 떨어졌는지를 모든 사람들이 일관되게 표현하도록 통일했다면, 이 벌어진 정도라는 "각도"라는 것도 일정한 기저에 따라 정의하여 모든 사람들이 같은 표현, 같은 크기를 이야기하게 하면 편하지 않을까? 이러한 발상에서 각도를 다음과 같이 재정의 하게 된다. 

 

각도 = 두 직선이 벌어진 정도 ⇒ 반지름이 1(기저)인 호의 길이 

 

각도를 길이로 재정의했으므로, 더 이상 한 바퀴는 360도가 아니게 된다. 360도는 그 자체가 원이 되므로, 반지름이 1인 원의 둘레 길이인 $ 2\pi$가 된다. 따라서, 지금까지 360도로 표현했던 것을 이제는 $2\pi \, \mathbf{rad}$로 표현하기로 약속하게 되고, 이를 "라디안법", 우리나라에서는 "호도법"이라고 부른다. 뒤에 rad를 붙힘으로써 단순한 숫자인 $2\pi$와 구분하려고 한다.

 

이제 위에서, 유클리드 평면에서의 기저를 이용해 원점에서 $x$축으로 4만큼 $y$축으로 3만큼 떨어진 점을 $(4e_0, \, 3e_1)$으로 표현했듯이, 라디안이라는 기호를 쓰기 위해서는 라디안 역시 그 기저인 $1\mathbf{rad}$를 정해야한다. 반지름의 길이가 1인 원의 둘레( $\ell$ )가 곧 호도법으로 360도를 나타내는 $2 \pi \, \mathbf{rad}$이라고 했으므로, 

 

$$ \begin{align} & \; \ell = 2 \pi \, \mathbf{rad} \\ \\ \Leftrightarrow \; & \frac{\ell}{2\pi} = 1 \, \mathbf{rad} \end{align} $$

 

반지름의 길이가 1인 경우 $\ell = 2\pi$이므로, 결국 $1 \, \mathbf{rad} = 1 $이 된다. 위 식에서 1은 호의 길이 1, 1rad은 중심각 1을 말한다. 아래 그림을 살펴보면

결국 "호의 길이"가 1이 되는 부채꼴의 중심각을 $1 \, \mathbf{rad}$이라고 정의할 수 있다. 하지만 원의 반지름이 1인 경우에만 생각해서는 의미가 없는 법. 이제 반지름의 길이가 $r$이면서 중심각은 똑같이 $1 \, \mathbf{rad}$인 경우에는 호의 길이가 어떻게 될까? 

중심각이 1 rad으로 같은 반지름이 1인 원과 반지름이 r인 원이 있다. 1 rad을 우리가 흔히 쓰는 º(degree, 도)인 θº라고 한다면, 중심각 θº는 다음과 같이 구할 수 있다.

 

$$ 1 = 2\pi \cdot 1 \cdot \frac{\theta}{360^\circ}  $$

$$ \frac{\theta}{360^\circ} = \frac{1}{2 \pi} $$

 

중심각은 1 rad으로 같은 채로 반지름이 r이므로, 우리가 구하고자 하는 호의 길이 $\ell$은

 

$$ \begin{align} \ell & = 2 \pi \cdot r \cdot \frac{\theta}{360} \\ \\ & = 2\pi \cdot r \cdot \frac{1}{2\pi} \\ \\ & = r \end{align} $$

 

신기하게도 반지름이 $r$일 때, 그 중심각이 1 rad이면, 호의 길이는 반지름과 같은 $r$이 된다. 즉, 중심각이 1 rad이라는 것은 반지름의 길이와 호의 길이가 같다는 것을 의미한다. 반대로, 반지름의 길이와 호의 길이가 같다면, 그 중심각은 1 rad이다.

 

 

라디안을 이용해 호의 길이를 구해보자

우선 다시 한번 우리가 배웠던 호의 길이를 구하는 식을 살펴보자. 중심각이 $a^\circ$인 부채꼴의 호의 길이 $\ell$은

$$ \begin{align} \ell & = 2\pi \cdot r \cdot \frac{a}{360} \\ \\ & = ( 2 \pi \cdot \frac{a}{360} ) \cdot r \end{align} $$

즉, 중심각인 $a$가 일정하다면, 호의 길이 $\ell$은 반지름 $r$에 비례한다. 

반지름이 $r$이고, 중심각이 $\theta\, \mathbf{rad}$인 부채꼴이 있다. 그렇다면, 지금까지 우리가 살펴본 내용을 토대로 다음과 같이 이야기할 수 있게 된다. 

 

반지름이 1이면서, 중심각이 $\theta \, \mathbf{rad}$인 부채꼴의 호의 길이는 $\theta$이다

↕

중심각이 같다면, 호의 길이는 반지름의 길이에 비례한다

↕

반지름이 $r$이면서 중심각이 같다면, 호의 길이도 똑같이 $r$배 늘어난다

↕

$\ell = r \theta$

 

분명 "라디안"으로 시작했지만, 마지막 호의 길이 $\ell$은 rad이 아닌 반지름 $r$과 반지름이 1인 경우의 호의 길이 $\theta$의 곱, 즉, 중심각만 같다면 길이의 관계만으로도 호의 길이를 구할 수 있다. 다시 말해, 원에서는 반지름이 1이면서 중심각이 $a$ rad인 부채꼴의 호의 길이($=a$)가 기저(basis)가 된 것이다. 여기서 중요한 점은 각도가 아닌 길이가 기저가 됐다는 점이다. 모든 부채꼴의 호의 길이는 위의 기저($\theta$)의 $k$배(정확히는 반지름 $r$배)로 표현할 수 있다는 뜻이며, 각도를 나타내던 단위 "rad"은 이제 사용하지 않아도 된다는 것을 의미한다. 길이의 관계로 표현할 수 있으니 말이다. 

 

예를 들어, 중심각이 60º인 부채꼴이 있다고 해보자. 그렇다면 위의 성질에 따라 "반지름이 1이면서 중심각이 $a \, \mathbf{rad}$(60º)인 호의 길이가 기저"가 된다. 따라서, 중심각이 60º인 호의 길이 $\ell$은

 

$$ \ell = 2 \pi \cdot 1 \cdot \frac{60}{360} = \frac{\pi}{3} $$

 

즉, 중심각이 $\dfrac{\pi}{3} \, \mathbf{rad} $인 모든 부채꼴의 호의 길이는 반지름 $r$에 따라, $\dfrac{\pi}{3} r$이 된다. 공식으로 외울 필요가 없다. $a^\circ$로 표현되는 모든 각은 이를 중심각으로 하고 반지름이 1인 호의 길이를 구하면, 그것이 곧, 호도법으로 표현한 중심각이 된다. 중심각이 53º라면, 라디안으로는 $\dfrac{53 \pi}{180}$가 된다.

 

따라서, 이제부터는 중심각을 표현할 때 rad이라는 단위를 무조건 빼고 표현하기로 한다.

 

그럼 왜 라디안법을 사용하는 것일까?

우리는 삼각비와 라디안을 이용하여 궁극적으로 삼각함수까지 개념을 넓혀가고자 한다. 삼각비가 아닌 삼각함수, 즉, 함수로 개념을 확장한다는 것은 $x$축에 해당하는 정의역의 범위를 실수 전체로 확장하고 싶다는 이야기와 같다. 그런데, 이렇게 가정할 경우 한가지 문제가 발생하는데, 

정의역의 범위를 확장하고 싶어도 기본적으로 삼각비의 전제 조건이 "직각삼각형"이라는 점이 문제가 된다. 왼쪽과 같이 예각의 범위 안에서는 삼각비를 정의할 수 있지만, 오른쪽과 같은 둔각삼각형의 경우에는 애초에 직각삼각형이 될 수 없으므로 삼각비를 어떻게 정의해야 할지에 대해서도 고민이 생긴다. 왼쪽으로 뻗은 직각삼각형으로 보기에는 왼쪽의 직각삼각형과 완전히 똑같은 상황이 된다. 이마저도 180º 안에서는 둔각삼각형이라도 만들어지지, 180º가 넘어가는 각도에 대해서는 삼각형 자체가 정의되지 않게 된다. 삼각형의 세 내각의 합은 180º를 넘을 수 없기 때문이다. 

 

그렇다면, 이를 어떻게 함수로 확장해 나가야할까? 이를 위해 라디안법이 필요하다.

중심각은 $\theta$로 같은 두 직각삼각형은 이전 포스팅에서 살펴본 바와 같이 그 비율이 일정한데

$$ \frac{a}{r} = \frac{a'}{r'} $$

위 식의 양변에 $\dfrac{1}{\theta},\, (\theta \neq 0)$를 곱하면,

$$ \begin{align} & \frac{a}{r \theta} = \frac{a'}{r' \theta} \\ \\ \Leftrightarrow \; & \frac{a}{\ell} = \frac{a'}{\ell '} \end{align} $$

빗변과 높이의 비율이 일정하다면, 같은 끼인각을 중심각으로 같는 호의 길이와 높이의 비율도 똑같다는 것을 알 수 있다. 물론 이 값이 애초에 우리가 삼각비로 설정한 빗변과 높이의 비율과는 조금 다르더라도 말이다. 

 

이러한 식의 변환은 단순히 변수를 가지고 곱하고 더하면서 장난친 것 같지만, 빗변이라는 삼각형에서만 존재하는 개념을 지웠다는 것에서 아주 큰 의미를 갖는다. 우리가 구하려고 했던 비율, 끼인각 θ에 따른 빗변과 높이의 비율을 $\sin{\theta}$로 표현하기로 하고 식을 다시 따져보면

$$ \sin{\theta} = \frac{a}{r} = \frac{a}{\ell} \cdot \theta $$

라고도 표현할 수 있게 된다. 아래의 그림을 살펴보자.

삼각형의 한 각이 위의 $\theta$인 삼각형은 존재할 수 없다. 삼각형의 내각의 합은 180º이므로, 180º를 넘어가는 각에 대해서는 빗변이라는 개념 자체가 존재할 수 없기 때문. 하지만, 빗변 $r$과의 관계가 아닌, $\sin{\theta} = \dfrac{a}{\ell} \cdot \theta$를 이용하면, 호의 길이는 180º를 넘어서도 정의할 수 있으므로, 삼각형이 아니더라도 삼각비를 정의할 수 있게 된다. 

 

이 때, 우리가 알고 있는 기본적인 각도의 단위인 degree(º)를 사용하게 되면 $\sin{\theta}$에 관여하는 변수가 각도, 길이로 두 개가 되지만, 라디안법을 사용하면 오롯이 $\sin{\theta}$에 관여하는 변수가 길이로 모두 통일된다. 기저를 2개에서 1개로 줄이는 것, 2차원 함수를 1차원 함수로 단순화한다는 것은, 단순히 고등과정에서의 계산 뿐만 아니라, 초월함수의 미분 등에서도 계산을 단순화하는데 큰 도움이 된다. 또 1라디안은 어찌됐든 그 호의 "길이"가 1이라는 것, 모든 유클리드 공간 안에서의 대수적 표현은 1을 기준으로 하므로, $\sin{e^x}$ 같은 말도 안될 것 같은 표현도 정의할 수 있다는 것을 의미한다. 하지만 이는 이번 문제를 푸는데 상관이 없으므로 넘어가기로 하고, 우리는 이것 하나만 여기서 기억하기로 하자. 

 

"삼각비, 삼각함수를 사용할 때에는 "호도법"을 사용하기로 한다"

 

다시 말해, $90^\circ = \dfrac{\pi}{2}$, $180^\circ = \pi $ … 로 표현하겠다.

 

이제 삼각함수로의 확장만이 남았다...

 

---

다음 글

2025.04.19 - [수학 이야기] - 중학생이 풀어보는 수능 수학 - 2025학년도 대학수학능력시험 수학영역 6번, 좌표와 삼각함수, 삼각비의 함수로의 확장(극좌표계)

중학생이 풀어보는 수능 수학 - 2025학년도 대학수학능력시험 수학영역 6번, 좌표와 삼각함수, 삼