2025학년도 대학수학능력시험 수학영역 6번 (2025. 11. 14.)
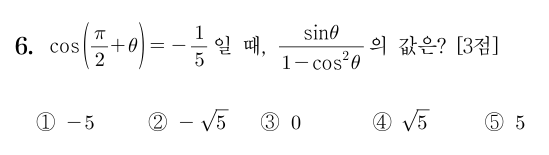
처음으로 기하파트의 문제가 나왔다. 사실 삼각함수는 대수에 가까운가, 기하에 가까운가에 대한 이야기는 다를 수 있지만, 적어도 교육과정에서의 설명은 기하를 기반으로 하고 있다. 즉, 삼각함수의 이해를 위해선 그래프, 그림 들을 이해하는 것을 기반으로 한다는 점을 꼭 알고 있어야 한다. 이 점이 너무나도 당연한 이야기 같지만, 생각보다 너무나도 무시되는 개념 중 하나이기도 하다.
그럼 삼각함수 시작
삼각형에 대한 기호 정리

먼저 삼각형의 기호를 어떤식으로 붙히는지에 대해서 살펴보자. 삼각형(三角形)이란, 세 개(三)의 각(角)을 가지도 있는 도형(形)이라는 뜻으로, 삼각형은 반드시 꼭짓점을 3개를 갖는데, 이 꼭지점들은 각각 영어 대문자로 표시한다(A, B, C). 그리고 이 꼭짓점 3개로 이루어진 삼각형을 △ABC라고 표현한다.
그리고 꼭짓점 3개로 이루어진 도형이므로, 반드시 3개의 변을 갖게 되는데 이 때, 각 꼭짓점의 반대편에 있는 변(이를 "대변"이라고 한다.)은 해당 꼭짓점 기호의 소문자로 표현한다. 위의 그림의 경우에는 꼭짓점 A의 대변은 $\overline{BC}$인데 이를 a라고 부를 수도 있다.
각(角)이란, 두 변이 서로 만날 때 생기는 점(꼭짓점)을 기준으로 두 변이 서로 얼마나 벌어져 있는지를 나타내는 것으로, 꼭짓점 C를 기준으로 하는 경우, 중등과정에서는 보통 ∠ACB 또는 ∠BCA로 표현하는데, 삼각형에서는 보조선을 따로 긋지 않는 한, 한개의 꼭짓점이 하나의 각을 가지므로 단순하게 ∠C라고 표현하거나 로마자 소문자인 α, β, γ 등으로 표현하기로 하자.
이러한 기호의 약속을 기반으로 삼각비에 대해서 설명을 시작
삼각형의 닮음
수학이 아닌 상식선에서, 우리는 어떤 경우를 닮았다고 하는가? 아래의 그림을 살펴보자.

강아지 그림들은 서로 크기가 다르기 때문에 똑같다고 말하지는 않지만, 사실 크기만을 제외하면 모두 똑같은 강아지 그림이다. 따라서 완전히 똑같다고는 말할 수 없어도 비슷하다고는 할 수 있다. 하지만 사자 그림은 아예 다른 그림으로 이 둘을 비슷하거나 닮았다고 하지는 않을 것이다. 이렇듯 닮았다는 것은 완벽히 똑같은 것은 아니지만, 비슷한 모습을 하고 있다는 것을 의미한다.
기하학(in 유클리드)에서는 닮음을 "크기와 상관없이 모양이 같은 상태"를 의미한다. 그럼 "모양이 같은 상태"란 무엇인가? 아주 간단한 이 문장 하나가 생각보다 꽤나 심오한 문제이기도 하다. 유클리드평면에 한정해서 하는 이야기라서 그렇지 대학과정으로 넘어가 위상의 개념 안에서는 도너츠, 머그컵, 빨대, 반지, 꽈배기가 모두 닮음이다. 아니 그런 걸 떠나서 우리가 중등 과정에서 배우는 평면에서도 닮음을, 모양이 같다는 것은 어떻게 정의할 것인가? 특히, 우리의 궁극적인 목표는 삼각함수이므로, 유클리드 평면에서의 삼각형이 닮았다는 것은 어떻게 정의할 것인가?

왼쪽의 그림은 각도를 유지한 채, 한변의 길이를 정확히 2배로 증가시킨 모습이다. 누가 보더라도 왼쪽의 삼각형은 크기는 다를지언정 서로 닮았다고 하기에 충분할 정도로 모양이 같아 보인다. 오른쪽은 넓이가 같지만(=높이가 같다, 크기가 같다), 삼각형을 이루는 각의 크기다 다르다. 각이 다르다보니, 크기가 같아도 이 두 삼각형이 서로 닮았다는 느낌이 전혀 들지 않는다. 이를 통해 우리는 다음을 알 수 있다.
"삼각형은 변의 길이가 크기를 결정하고, 각도가 모양을 결정한다."
↓
"삼각형의 세 각의 크기가 같으면 모양은 같다 ⇒ 닮았다"
크기와 상관없이 모양이 같은 것을 닮았다고 하기로 했으니, 왼쪽의 그림처럼 각도는 모두 같은 상태에서 한 변의 길이가 일정 비율만큼 늘었다면, 나머지 변은 어떻게 변하는지 한번 살펴보기로 하자.

전제조건은 "모양은 비슷하므로 세 각이 모두 같다."이므로, 자연스럽게 $\angle C = \angle C'$, 위와 같이 $C$를 기준으로 완벽하게 겹쳐지게 된다. 또한, 전제조건에 의해 $\angle B = \angle B'$로, $\overline{AB} \parallel \overline{A'B'}$(평행)이다. 평행선 입장에서는 동위각이 같기 때문.
이쯤에서 우리가 증명하고자 하는 내용을 다시 한번 짚어보자.
검은색 삼각형(△ABC)과 파란색 삼각형(△A'B'C')의 세 각이 모두 같은 상태에서, $\overline{BC}(= a)$를 $\overline{B'C}(= a+a')$로 $k$배 늘렸을 때, 다른 변들, 여기에서는 특히 $\overline{A'C}(= b+b')$도 $\overline{AC}(= b)$의 $k$배가 될 것인가? 다시 말해, 같은 비율로 변화할 것인가 확인하고자 한다
이를 위해 오른쪽 그림과 같이 $\overline{AB'}, \, \overline{A'B}$ 보조선을 긋어보자

왼쪽의 그림을 보면 $\triangle{ABC}, \, \triangle{AA'B}$의 높이는 모두 같으므로 사실상 두 삼각형의 넓이 비는 밑변의 비와 같다.
$$ \begin{align} \triangle{ABC} : \triangle{AA'B} & = \frac{1}{2} \cdot \overline{AC} \cdot h : \frac{1}{2} \cdot \overline{AA'} \cdot h \\ \\ & = \cancel{\frac{1}{2}} b \cancel{h} : \cancel{\frac{1}{2}} b' \cancel{h} \\ \\ & = b : b' \end{align} $$
비례식에서 외항, 내항의 곱은 서로 같기 때문에, 식을 두 그림의 공통부분인 △ABC에 관하여 나타내면,
$$ b' \cdot \triangle{ABC} = b \cdot \triangle{AA'B} \; \Rightarrow \; \triangle{ABC} = \frac{b}{b'} \cdot \triangle{AA'B} \cdots (1)$$
같은 원리로 오른쪽의 그림도 다음과 같이 표현할 수 있다.
$$ \triangle{ABC} : \triangle{ABB'} = a : a' $$
$$ \Rightarrow \triangle{ABC} = \frac{a}{a'} \cdot \triangle{ABB'} \cdots (2) $$
(1), (2)를 △ABC에 관하여 연립하면
$$ \frac{b}{b'} \cdot \triangle{AA'B} = \frac{a}{a'} \cdot \triangle{ABB'} \cdots (3)$$

그런데, 자세히 보면, 보조선을 그어서 만든 두 삼각형 $\triangle{AA'B}, \, \triangle{ABB'}$는 밑변이 $c$이고 $\overline{AB} \parallel \overline{A'B'}$이므로 높이가 서로 같기 때문에, 두 삼각형의 넓이는 같다.
$$ \triangle{AA'B} = \triangle{ABB'} $$
이를 (3)에 적용시키면
$$\begin{align} & \quad \frac{b}{b'} \cdot \cancel{\triangle{AA'B}} = \frac{a}{a'} \cdot \cancel{\triangle{ABB'}} \\ \\ \Rightarrow & \quad \frac{b}{b'} = \frac{a}{a'} \end{align}$$
우리가 궁금한 것은 $ ak = a+a'$ 일 때, $bk = b+b' $ 일까? 이다.
$a, \; b \neq 0$이므로,
$$ k = \frac{a+a'}{a} = 1 + \frac{a'}{a} = 1 + \frac{b'}{b} = \frac{b+b'}{b} $$
따라서, $ bk = b+b'$이다.
즉, 삼각형의 모든 각이 같은 상태에서 한 변을 $k$배 늘렸더니 다른 변도 $k$배 늘어났다는 것을 의미한다. 즉,
"두 삼각형의 세 각의 크기가 같다 ⇒ 두 삼각형에 대응되는 세 쌍의 변의 길이의 비가 같다"
$$(a:a' = b:b' = c:c')$$
추가로 위의 내용은 ∠C가 90도보다 크더라도 똑같은 방식으로 증명할 수 있으므로, 모든 삼각형에 동일하게 적용된다.
그럼 반대로 세 쌍의 변의 길이 비가 같으면, 두 삼각형의 세 각의 크기는 같을까? 이를 보이기 위해선 삼각형의 유일성에 대해서 하나 이야기하고 가자.
"세 변의 길이가 정해져 있다면, 이를 통해 만들 수 있는 삼각형은 유일하다.(한 개만 만들 수 있다.)"
작도법을 통해 충분히 증명이 가능하므로, 이에 대한 증명은 넘기도록 한다. 하고자 하는 말은 결국 세 변의 길이가 같은 두 개의 삼각형은 존재할 수 없기 때문에, 세 변의 길이가 모두 같다면, 그 두 삼각형은 사실 같은 것이라는 것.
그래서 "삼각형을 유일하게 결정하는 조건 = 삼각형이 서로 같을 조건"을 보통 삼각형이 "합동이 될 조건"으로 배운다. 세 변의 길이가 정해져 있다는 SSS합동을 이야기 하는 것과 같다.
두번째로는 아래 그림을 살펴보자.
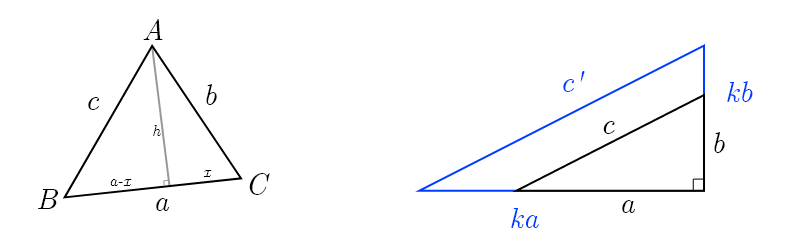
먼저, 위에서 살펴봤었던 삼각형을 그대로 가지고 왔다. 우리가 알고 싶은 건 "세 변의 길이가 같은 비율로 변하면, 삼각형의 세 각은 같을까? = 그대로 유지될까?" 이다. 닮음을 보이고자 하는 것이니 닮음을 이용한 성질들을 철저히 배제하고 이를 보여야 한다는 제약이 제일 크다. 예를 들어 평행선과 선분의 비율을 이용한다던지(대표적인 삼각형의 닮음을 이용하여 증명하는 성질) 등의 간편한 방법을 아예 없다고 생각하고 살펴보아야 한다는 것이다.
따라서, 우리는 피타고라스의 정리를 이용하고자 한다. 오른쪽 삼각형의 a, b, c로 이루어진 직각삼각형은 다음의 산식을 만족한다.
$$ c^2 = a^2 + b^2 \quad (a, b, c \in \triangle{ABC}) $$
이 때, 변 a, b를 이 둘의 끼인각인 직각을 유지한 채로 각각 $k$배 만큼 변화시킨다면, $ a \rightarrow ka, \, b \rightarrow kb$로 오른쪽 그림과 같이 변하게 될 것이다. 그렇다면 이에 따라 변하게 된 c'는 과연 c의 몇 배일까?
$$ \begin{align} c' & = \sqrt{(ka)^2 + (kb)^2} \\ \\ & = \sqrt{k^2 (a^2 + b^2)} \\ \\ & = k \sqrt{a^2 + b^2} \quad (\because k>0) \\ \\ & = kc \end{align} $$
그럼 직각인 부분이 아니어도 그럴까?

먼저 왼쪽 그림을 살펴보자. 끼인각을 공유하고 있는 상태에서 b, c를 k배 늘리면, $a = \sqrt{c^2 - b^2}$ 이므로
$$ a' = \sqrt{(kc)^2 - (kb)^2} = ka $$
과정은 모두 동일하므로 결과만 나타냈다. 결론은 왼쪽도 오른쪽도 모두 k배 된다는 사실이다.
여기서 우리는 모든 삼각형이 그런지는 알 수 없지만, 적어도 직각삼각형에서만큼은
"직각삼각형의 임의의 두 변을 일정 비율만큼 변화시키면 나머지 한 변도 같은 비율만큼 변화하게 된다."
는 사실이다. 세 변을 모두 같은 비율로 변화시키는 것과, 두 변만 같은 비율로 변화시켰더니 나머지 한 변이 무조건 같은 비율로 종속적으로 변한다는 것은 완전히 다른 이야기이다.

그렇다면, $\angle B$를 기준으로 $\overline{AB}$ 방향, $\overline{BC}$ 방향으로 $k$배씩 변화시켰다고 해보자. 우선 $\triangle{ABC}$는 직각삼각형이므로 $a^2 + b^2 = c^2$을 만족한다. 그리고 직각삼각형의 두 변을 $k$배 변화시키면 나머지 한 변도 같은 비율로 변한다고 했기 때문에, $\overline{A'C'}$는 $\overline{AC} (= b)$의 $k$배$(=kb)$가 된다.
아래 변 a를 k배 했다고 해서 ∠C'가 직각임을 보장하지는 않는다. 그런데,
$$ \begin{align} (ka)^2 + (kb)^2 & = k^2 (a^2 + b^2) \\ \\ & = k^2 c^2 = (kc)^2 \end{align} $$
즉, c를 빗변으로 하는 피타고라스의 정리를 만족하기 때문에 $k$배 변화시키고 보니 $\overline{A'B}$를 빗변으로 하는 새로운 직각삼각형도 된 것이다. 결국 동위각이 같기 때문에 $\overline{AC} \parallel \overline{A'C'}$, 평행선의 성질에 따라 자연스럽게 $\angle A = \angle A' $이 된다.

그럼 이제 본래 삼각형을 살펴보자. 기존의 검은색 삼각형(△ABC)에 대해서, 점 A에서 $\overline{BC}$에 내린 수선의 발을 H라고 하면, 원래의 삼각형은 두 개의 직각삼각형 △ABH, △ACH로 나뉘게 된다.
먼저 △ABH에 대해, ∠BAH를 기준으로 $\overline{AB}, \, \overline{AH}$를 k배 변화시키면, 위에서 지금까지 살펴본 바와 같이 다음을 만족하게 된다.
$$ \overline {BH} \parallel \overline {B'H'} \; \Rightarrow \; \angle B = \angle B' $$
$$ \overline{B'H'} = k \cdot \overline{BH}= k(a-x) $$
같은 방식으로 △ACH에 대해서도 아래의 조건을 만족하게 된다.
$$ \angle C = \angle C' $$
$$ \overline{C'H'} = kx$$
따라서,
$$\begin{align} \overline{B'C'} & = \overline{B'H'} + \overline{C'H'} \\ \\ & = k(a-x) + kx = ka \end{align} $$
결국 직각삼각형이 아니더라도, 두 변을 같은 비율만큼 변화시키면 나머지 하나도 같은 비율로 변하게 된다.
지금까지 살펴 본 내용을 정리하면
1. $\overline{AB}$와 $\overline{AC}$를 $k$배 변화시켜서 만든 $\triangle{AB'C'}$와 본래의 $\triangle{ABC}$는 세 각이 모두 같다.
2. 이렇게 만들어진 $\triangle{AB'C'}$의 각 변의 길이는 $ka, \, kb, \, kc$이다.
2번의 사실이 이제 중요해졌다. 이렇게 만들어 놓고 보니, 우리가 애초에 가정했던 "모든 변을 일정 비율만큼 늘린(k배) 삼각형"이 됐다. 이건 내가 임의로 만든 삼각형 아닌가? 맞다. 임의로 만든 삼각형이다. 그런데, 만들고 보니 놀랍게도 똑같은 삼각형이 됐다. 임의로 만들었으니 길이만 같은 다른 삼각형이 아니냐 반문할 수 있지만, 맨 처음 언급한대로 "길이가 정해졌다면, 만들 수 있는 삼각형은 유일"하다.
즉, 일정 비율만큼 변화시킨 오른쪽의 파란색 삼각형은 사실 왼쪽의 검은색 삼각형을 통해 만든 △AB'C'와 완전히 같은 삼각형이다. 그리고 이 삼각형은 위의 1번 성질을 만족한다. 따라서
"두 쌍의 변의 길이를 같은 비율로 변화시킨다 = 세 쌍의 변의 길이의 비가 같다 ⇒ 두 삼각형의 세 각의 크기가 같다"
"∠A = ∠A' , ∠B = ∠B' , ∠C = ∠C' "
위에서 이 명제의 역이 성립함도 보였었다. 결국
"두 삼각형에 대응되는 세 쌍의 변의 길이의 비가 같다 ⇔ 두 삼각형의 세 각의 크기가 같다"
그리고 사실 중간에 두 변의 비율을 조정시키면서 마지막 닮음의 조건인 "두 쌍의 변의 길이의 비와 끼인각이 같다 ⇔ 세 쌍의 변의 길이의 비가 같다"는 사실도 증명한 것이나 다름없다. 그러므로
두 삼각형에 대응되는 세 쌍의 변의 길이의 비가 같다(SSS)
↓↑
두 삼각형의 두 쌍의 변의 길이의 비와 끼인각이 같다(SAS)
↓↑
두 삼각형의 세 각의 크기가 같다(AA)
↓↑
삼각형이 닮음이다
사실 중등과정에서 닮음을 이렇게 다루지는 않는다. 하지만, 누군가는 삼각형의 닮음을 배우면서 한번쯤은 가져봤을 질문들이 있다. "세 각이 같다고 두 삼각형이 닮은 건가?, 같은 비율로 늘렸다고 그 내각들이 전부 그대로 유지될까?". 이런 의심을 한다는 것 자체가 수학을 잘 할 수 있는 기본 마인드는 갖춰졌다는 것을 의미한다.
사실 중등교육과정에서 닮음의 이유에 대해서는 굳이 생각할 필요가 없고, 앞으로 다룰 삼각비, 삼각함수를 이해하는 데에도 닮음의 이유를 굳이 알아야 할 필요는 없지만, 당연하다고 받아들였던 것을 당연하다고 생각지 않고 반례를 탐구해보는 것이 수학을 하는 입장에서는 꽤나 좋은 마인드가 될 수 있다.
결국 닮음의 진정한 정의를 위에서는 각이 같음을 기준으로 설명했지만, 반대로 누군가는 "세 변의 길이를 같은 비율로 늘리거나 줄였을 때 닮았다고 하는 거지 무슨소리야!" 라고 할 수도 있다. 하지만 이는 의미없는 논쟁이다. 왜냐, 같은 비율로 늘리거나 줄이면, 결국 내각이 모두 같기 때문이다. 즉, 같은 이야기를 다르게 표현하고 있을 뿐인 것이다
다음 글
2025.03.03 - [수학 이야기] - 중학생이 풀어보는 수능 수학 - 2025학년도 대학수학능력시험 수학영역 6번, 피타고라스 정리와 삼각비, 삼각형의 모든 정보를 담다
중학생이 풀어보는 수능 수학 - 2025학년도 대학수학능력시험 수학영역 6번, 피타고라스 정리와
2025학년도 대학수학능력시험 수학영역 6번 (2025. 11. 14.)이전 글2025.02.20 - [수학 이야기] - 중학생이 풀어보는 수능 수학 - 2025학년도 대학수학능력시험 수학영역 6번, 삼각형의 닮음 조건은 이유가
wkqtkdtlr.tistory.com



